| Date | November 2010 | Marks available | 5 | Reference code | 10N.2.SL.TZ0.B1 |
| Level | Standard level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Calculate and Show that | Question number | B1 | Adapted from | N/A |
Question
This question is in two parts. Part 1 is about a simple pendulum. Part 2 is about the Rutherford model of the atom.
Part 1 Simple pendulum
A pendulum consists of a bob suspended by a light inextensible string from a rigid support. The pendulum bob is moved to one side and then released. The sketch graph shows how the displacement of the pendulum bob undergoing simple harmonic motion varies with time over one time period.
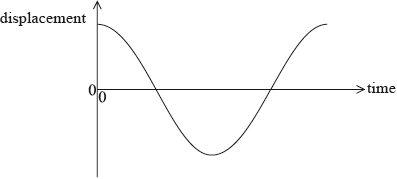
On the sketch graph above,
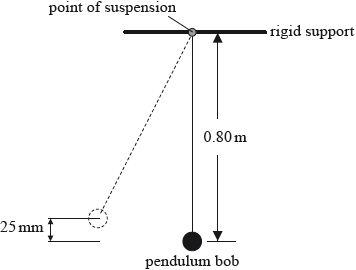
A pendulum bob is moved to one side until its centre is 25 mm above its rest position and then released.
The point of suspension of a pendulum bob is moved from side to side with a small amplitude and at a variable driving frequency \(f\).
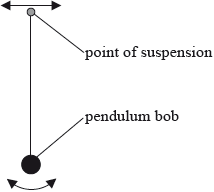
For each value of the driving frequency a steady constant amplitude \(A\) is reached. The oscillations of the pendulum bob are lightly damped.
Part 2 Rutherford model of the atom
The isotope gold-197 \(\left( {_{\;79}^{197}Au} \right)\) is stable but the isotope gold-199 \(\left( {_{\;79}^{199}Au} \right)\) is not.
(i) label with the letter A a point at which the acceleration of the pendulum bob is a maximum.
(ii) label with the letter V a point at which the speed of the pendulum bob is a maximum.
Explain why the magnitude of the tension in the string at the midpoint of the oscillation is greater than the weight of the pendulum bob.
(i) Show that the speed of the pendulum bob at the midpoint of the oscillation is \({\text{0.70 m}}\,{{\text{s}}^{ - 1}}\).
(ii) The mass of the pendulum bob is 0.057 kg. The centre of the pendulum bob is 0.80 m below the support. Calculate the magnitude of the tension in the string when the pendulum bob is vertically below the point of suspension.
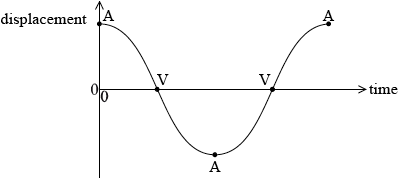
(i) On the axes below, sketch a graph to show the variation of \(A\) with \(f\).

(ii) Explain, with reference to the graph in (d)(i), what is meant by resonance.
The pendulum bob is now immersed in water and the variable frequency driving force in (d) is again applied. Suggest the effect this immersion of the pendulum bob will have on the shape of your graph in (d)(i).
Most alpha particles used to bombard a thin gold foil pass through the foil without a significant change in direction. A few alpha particles are deviated from their original direction through angles greater than 90°. Use these observations to describe the Rutherford atomic model.
(i) Outline, in terms of the forces acting between nucleons, why, for large stable nuclei such as gold-197, the number of neutrons exceeds the number of protons.
(ii) A nucleus of \(_{\;{\text{79}}}^{{\text{199}}}{\text{Au}}\) decays to a nucleus of \(_{\;{\text{80}}}^{{\text{199}}}{\text{Hg}}\) with the emission of an electron and another particle. State the name of this other particle.
Markscheme
(i) one A correctly shown;
(ii) one V correctly shown;
pendulum bob accelerates towards centre of circular path / OWTTE;
therefore force upwards;
that adds to tension produced by the weight;
(i) evidence shown of equating kinetic energy and gravitational potential energy;
\(v = \sqrt {(2 \times 9.8 \times 0.025)} \);
\( = 0.70{\text{ m}}\,{{\text{s}}^{ - 1}}\)
Allow g = 10 m\(\,\)s–2 answer 0.71 m\(\,\)s–2.
(ii) centripetal acceleration \(\left( { = \frac{{{v^2}}}{r}} \right){\text{ }}\left[ { = \frac{{{\text{0.}}{{\text{7}}^{\text{2}}}}}{{{\text{0.8}}}}} \right] = 0.61{\text{ }}\left( {{\text{m}}\,{{\text{s}}^{ - 2}}} \right)\);
net acceleration \( = (9.81 + 0.61 = ){\text{ }}10.4{\text{ }}\left( {{\text{m}}\,{{\text{s}}^{ - 2}}} \right)\) or \(T-mg = m \times 0.61\);
\({\text{tension}} = (ma = ){\text{ }}0.59{\text{ N}}\);
Allow g = 10 m\(\,\)s–2 answer 0.60 N.
Award [3] for bald correct answer.
(i) 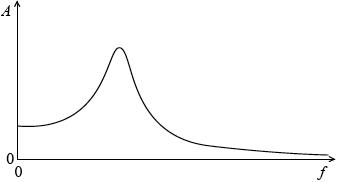
one maximum shown and curve broadly similar to example above;
amplitude falls on each side by lower amount on low driving frequency side;
(ii) resonance is where driving frequency equals/close to natural frequency;
the frequency at the maximum amplitude of the graph;
lower amplitude everywhere on graph;
with a much broader resonance peak;
maximum moves to left on graph;
Award [2] for a sketch graph.
most of the atom is empty space;
most of the mass/(protonic) charge of the atom is concentrated in the nucleus/nucleus is dense;
\(\begin{array}{*{20}{l}} \begin{gathered} {\text{nucleus is positively charged;}} \hfill \\ {\text{(most) alphas not close enough to nuclei to be deflected;}} \hfill \\ {\text{(very few) alphas (are) close enough to nuclei to be deflected;}} \hfill \\ \end{gathered} &{\left\{ \begin{gathered} These points can \hfill \\ be awarded to a \hfill \\ labelled diagram. \hfill \\ \end{gathered} \right.} \end{array}\)
To award the last two marking points for a diagram response the candidate must show that a non-deflected alpha is well away from a nucleus and a strongly deflected alpha is aimed very close or head-on.
(i) mention of Coulomb repulsion between protons;
mention of strong (nuclear) force (between nucleons);
overall balance must be correct (and more neutrons needed for this);
Award [0] for a statement that neutron is negative.
(ii) anti neutrino / \(\bar v\);
Examiners report
Identifications of points A and V were mixed. About half the candidates received both marks here.
This was poorly done with many misapprehensions evident. The main problem was that candidates failed to associate the effect with the presence of a centripetal force and also unable to consider it in terms of the directions and additions of the various forces in the situation.
(i) This was well done by many. However a use of a suvat equation is not appropriate in this case as the acceleration is not uniform.
(ii) Candidates who kept a clear head were able to arrive at a correct answer even if they had failed in part (b)
(i) Graphs were poor in general with few gaining both marks and many candidates unable to make any progress. Graphs often showed a decreasing amplitude against time despite the frequency label on the x-axis.
(ii) Few understood the meaning of the term “resonance” sufficiently to be able to describe it in terms of the graph.
Again, few candidates referred their answer to the graph. Some were able to gain credit for discussing changes in amplitude.
Candidates who rely on a diagram rather than a written description must ensure that their sketches give all the required information unambiguously. In this type of question it is also common to see candidates repeating part of the question itself back to the examiner; this will not gain credit. Candidates needed to distinguish between those alpha particles passing close to and those far away from a nucleus, and then to give the deduced properties of the nucleus from these observations. Descriptions were often illogical and repetitive.
Most candidates could write with confidence about the repulsive nature of the proton-proton interaction and the attractive nature of the strong nuclear force. Few gave good accounts of the balance between these two forces or described the energy situation (a better way to answer). Weak candidates could not name the strong nuclear force adequately.

