| Date | November 2014 | Marks available | 2 | Reference code | 14N.2.SL.TZ0.5 |
| Level | Standard level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Outline | Question number | 5 | Adapted from | N/A |
Question
This question is in two parts. Part 1 is about the oscillation of a mass. Part 2 is about nuclear fission.
Part 1 Oscillation of a mass
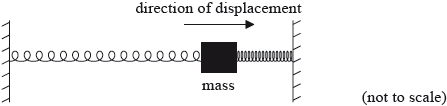
A mass of 0.80 kg rests on a frictionless surface and is connected to two identical springs both of which are fixed at their other ends. A force of 0.030 N is required to extend or compress each spring by 1.0 mm. When the mass is at rest in the centre of the arrangement, the springs are not extended.
The mass is displaced to the right by 60 mm and released.
The motion of an ion in a crystal lattice can be modelled using the mass–spring arrangement. The inter-atomic forces may be modelled as forces due to springs as in the arrangement shown.
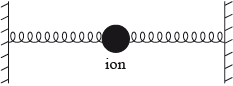
The frequency of vibration of a particular ion is \(7 \times {10^{12}}{\text{ Hz}}\) and the mass of the ion is \(5 \times {10^{ - 26}}{\text{ kg}}\). The amplitude of vibration of the ion is \(1 \times {10^{ - 11}}{\text{ m}}\).
Part 2 Nuclear fission
A reaction that takes place in the core of a particular nuclear reactor is as shown.
\[_{\;92}^{235}{\text{U}} + _0^1{\text{n}} \to _{\;56}^{144}{\text{Ba}} + _{36}^{89}{\text{Kr}} + 3_0^1{\text{n}}\]
In the nuclear reactor, \(9.5 \times {10^{19}}\) fissions take place every second. Each fission gives rise to 200 MeV of energy that is available for conversion to electrical energy. The overall efficiency of the nuclear power station is 32%.
In addition to the U-235, the nuclear reactor contains a moderator and control rods. Explain the function of the
Determine the acceleration of the mass at the moment of release.
Outline why the mass subsequently performs simple harmonic motion (SHM).
Calculate the period of oscillation of the mass.
Estimate the maximum kinetic energy of the ion.
On the axes, draw a graph to show the variation with time of the kinetic energy of mass and the elastic potential energy stored in the springs. You should add appropriate values to the axes, showing the variation over one period.

Calculate the wavelength of an infrared wave with a frequency equal to that of the model in (b).
Determine the mass of U-235 that undergoes fission in the reactor every day.
Calculate the power output of the nuclear power station.
moderator.
control rods.
Markscheme
force of 1.8 N for each spring so total force is 3.6 N;
acceleration \( = \frac{{3.6}}{{0.8}} = 4.5{\text{ m}}{{\text{s}}^{ - 2}}\); (allow ECF from first marking point)
to left/towards equilibrium position / negative sign seen in answer;
force/acceleration is in opposite direction to displacement/towards equilibrium position;
and is proportional to displacement;
\(\omega = \left( {\sqrt {\left( {\frac{a}{x}} \right)} = } \right){\text{ }}\sqrt {\frac{{4.5}}{{60 \times {{10}^{ - 3}}}}} {\text{ }}( = 8.66{\text{ rad}}\,{{\text{s}}^{ - 1}})\);
\(T = 0.73{\text{ s}}\);
Watch out for ECF from (a)(i) eg award [2] for \(T = 1.0{\text{ }}s\) for \(a = 2.25{\text{ m}}\,{{\text{s}}^{ - 2}}\).
\(\omega = 2\pi \times 7 \times {10^{12}}( = 4.4 \times {10^{13}}Hz)\);
\(5 \times {10^{ - 21}}{\text{ J}}\);
Allow answers in the range of 4.8 to \(4.9 \times {10^{ - 21}}{\text{ J}}\) if 2 sig figs or more are used.
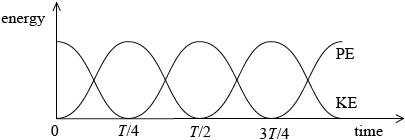
KE and PE curves labelled – very roughly \({\cos ^2}\) and \({\sin ^2}\) shapes; } (allow reversal of curve labels)
KE and PE curves in anti-phase and of equal amplitude;
at least one period shown;
either \({E_{\max }}\) marked correctly on energy axis, or \(T\) marked correctly on time axis;
\(7.0 \times {10^{12}}{\text{ Hz}}\) is equivalent to wavelength of \(4.3 \times {10^{ - 5}}{\text{ m}}\);
number of fissions in one day \( = 9.5 \times {10^{19}} \times 24 \times 3600{\text{ }}( = 8.2 \times {10^{24}})\);
mass of uranium atom \( = 235 \times 1.661 \times {10^{ - 27}}{\text{ }}( = 3.9 \times {10^{ - 25}}{\text{ kg)}}\);
mass of uranium in one day \(( = 8.2 \times {10^{24}} \times 3.9 \times {10^{ - 25}}) = 3.2{\text{ kg}}\);
energy per fission \( = 200 \times {10^6} \times 1.6 \times {10^{ - 19}}{\text{ }}( = 3.2 \times {10^{ - 11}}{\text{ J)}}\);
power output \( = (9.5 \times {10^{19}} \times 3.2 \times {10^{ - 11}} \times 0.32 = ){\text{ }}9.7 \times {10^8}{\text{ W}}\);
Award [1] for an answer of \(6.1 \times {10^{27}}{\text{ eV}}{{\text{s}}^{ - 1}}\).
neutrons have to be slowed down (before next fission);
because the probability of fission is (much) greater (with neutrons of thermal energy);
neutrons collide with/transfer energy to atoms/molecules (of the moderator);
have high neutron capture cross-section/good at absorbing neutrons;
(remove neutrons from the reaction) thus controlling the rate of nuclear reaction;
Examiners report
This is a slightly different situation. Most candidates at SL did not use F and m to find acceleration. Very few added the force due to each spring and ECF was frequently applied.
Care was needed in showing the constant and equal amplitudes. Many poor answers were seen.
Mostly good answers although it was rare to find a candidate who stated that the probability of further fusion is increased with thermal neutrons.
Too many answers lacked precision referring only to the use of control rods in avoiding an explosion or meltdown.

