| Date | May 2018 | Marks available | 1 | Reference code | 18M.3.SL.TZ2.4 |
| Level | Standard level | Paper | Paper 3 | Time zone | Time zone 2 |
| Command term | Calculate | Question number | 4 | Adapted from | N/A |
Question
When a spaceship passes the Earth, an observer on the Earth and an observer on the spaceship both start clocks. The initial time on both clocks is 12 midnight. The spaceship is travelling at a constant velocity with γ = 1.25. A space station is stationary relative to the Earth and carries clocks that also read Earth time.
Some of the radio signal is reflected at the surface of the Earth and this reflected signal is later detected at the spaceship. The detection of this signal is event B. The spacetime diagram is shown for the Earth, showing the space station and the spaceship. Both axes are drawn to the same scale.
Calculate the velocity of the spaceship relative to the Earth.
The spaceship passes the space station 90 minutes later as measured by the spaceship clock. Determine, for the reference frame of the Earth, the distance between the Earth and the space station.
As the spaceship passes the space station, the space station sends a radio signal back to the Earth. The reception of this signal at the Earth is event A. Determine the time on the Earth clock when event A occurs.
Construct event A and event B on the spacetime diagram.
Estimate, using the spacetime diagram, the time at which event B occurs for the spaceship.
Markscheme
0.60c
OR
1.8 × 108 «m s–1»
[1 mark]
ALTERNATIVE 1
time interval in the Earth frame = 90 × γ = 112.5 minutes
«in Earth frame it takes 112.5 minutes for ship to reach station»
so distance = 112.5 × 60 × 0.60c
1.2 × 10m12 «m»
ALTERNATIVE 2
Distance travelled according in the spaceship frame = 90 × 60 × 0.6c
= 9.72 × 1011 «m»
Distance in the Earth frame «= 9.72 × 1011 × 1.25» = 1.2 × 1012 «m»
[3 marks]
signal will take «112.5 × 0.60 =» 67.5 «minutes» to reach Earth «as it travels at c»
OR
signal will take «\(\frac{{1.2 \times {{10}^{12}}}}{{3 \times {{10}^8}}}\) =» 4000 «s»
total time «= 67.5 + 112.5» = 180 minutes or 3.00 h or 3:00am
[2 marks]
line from event E to A, upward and to left with A on ct axis (approx correct)
line from event A to B, upward and to right with B on ct' axis (approx correct)
both lines drawn with ruler at 45 (judge by eye)
eg:
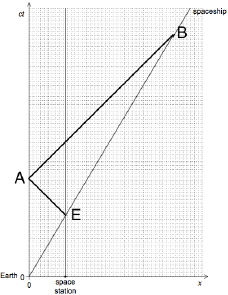
[3 marks]
ALTERNATIVE 1
«In spaceship frame»
Finds the ratio \(\frac{{OB}}{{OE}}\) (or by similar triangles on x or ct axes), value is approximately 4
hence time elapsed ≈ 4 × 90 mins ≈ 6h «so clock time is ≈ 6:00»
Alternative 1:
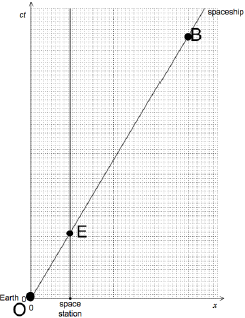
Allow similar triangles using x-axis or ct-axis, such as \(\frac{{distance\,2}}{{distance\,1}}\) from diagrams below
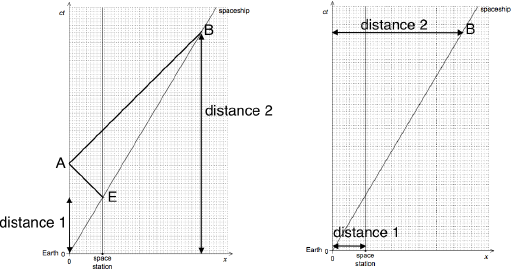
ALTERNATIVE 2
«In Earth frame»
Finds the ratio
\(\frac{{ct{\text{ coordinate of B}}}}{{ct{\text{ coordinate of A}}}}\), value is approximately 2.5
hence time elapsed ≈ \(\frac{{2.5 \times 3{\text{h}}}}{{1.25}}\) ≈ 6h
«so clocktime is ≈ 6:00»
ALTERNATIVE 2:
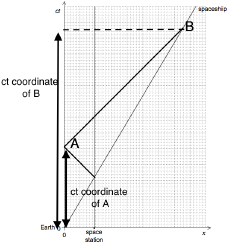
[2 marks]

