| Date | November 2010 | Marks available | 2 | Reference code | 10N.3.SL.TZ0.D1 |
| Level | Standard level | Paper | Paper 3 | Time zone | Time zone 0 |
| Command term | Show that | Question number | D1 | Adapted from | N/A |
Question
This question is about a Galilean transformation and time dilation.
Ben is in a spaceship that is travelling in a straight-line with constant speed \(v\) as measured by Jill who is in a space station.
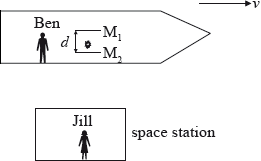
Ben switches on a light pulse that bounces vertically (as observed by Ben) between two horizontal mirrors \({{\text{M}}_{\text{1}}}\) and \({{\text{M}}_{\text{2}}}\) separated by a distance \(d\). At the instant that the mirrors are opposite Jill, the pulse is just leaving the mirror \({{\text{M}}_{\text{2}}}\). The speed of light in air is \(c\).
The time for the light pulse to travel from \({{\text{M}}_{\text{2}}}\) to \({{\text{M}}_{\text{1}}}\) as measured by Jill is \(\Delta t\).
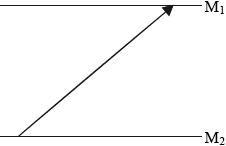
On the diagram, sketch the path of the light pulse between \({{\text{M}}_{\text{1}}}\) and \({{\text{M}}_{\text{2}}}\) as observed by Jill.

(i) State, according to Jill, the distance moved by the spaceship in time \(\Delta t\).
(ii) Using a Galilean transformation, derive an expression for the length of the path of the light between \({{\text{M}}_{\text{2}}}\) and \({{\text{M}}_{\text{1}}}\).
State, according to special relativity, the length of the path of the light between \({{\text{M}}_{\text{1}}}\) and \({{\text{M}}_{\text{1}}}\) as measured by Jill in terms of \(c\) and \(\Delta t\).
The time for the pulse to travel from \({{\text{M}}_{\text{2}}}\) to \({{\text{M}}_{\text{1}}}\) as measured by Ben is \(\Delta t'\). Use your answer to (b)(i) and (c) to derive a relationship between \(\Delta t\) and \(\Delta t'\).
According to a clock at rest with respect to Jill, a clock in the spaceship runs slow by a factor of 2.3. Show that the speed \(v\) of the spaceship is 0.90c.
Markscheme
any diagonal line as shown;
(i) \(v\Delta t\);
(ii) speed of pulse \({({c^2} + {v^2})^{\frac{1}{2}}}\);
distance \( = {({c^2} + {v^2})^{\frac{1}{2}}}\Delta t\);
Award [2] for bald correct answer.
\(c\Delta t\);
\(d = c\Delta t'\);
from Pythagoras \({d^2} = {c^2}\Delta {t'^2} = {c^2}\Delta {t^2} - {v^2}\Delta {t^2}\);
\(\Delta t = \frac{{\Delta t'}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\);
recognize that \(2.3 = \frac{1}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\);
some evidence of rearranging e.g. \(v = \sqrt {\frac{{{{[2.3]}^2} - 1}}{{{{[2.3]}^2}}}} \);
\( = 0.90{\text{c}}\)
Examiners report
Most candidates were able to draw the correct path of the light.
Parts (b), (c) and (d) effectively dealt with the derivation of the time dilation formula and here many candidates had problems often relying on guesswork and half-remembered proofs rather than follow the logical development of the questions. The calculation was often done well but with the usual confusion between the times.
Parts (b), (c) and (d) effectively dealt with the derivation of the time dilation formula and here many candidates had problems often relying on guesswork and half-remembered proofs rather than follow the logical development of the questions. The calculation was often done well but with the usual confusion between the times.
Parts (b), (c) and (d) effectively dealt with the derivation of the time dilation formula and here many candidates had problems often relying on guesswork and half-remembered proofs rather than follow the logical development of the questions. The calculation was often done well but with the usual confusion between the times.

