| Date | May 2017 | Marks available | 2 | Reference code | 17M.3.SL.TZ2.5 |
| Level | Standard level | Paper | Paper 3 | Time zone | Time zone 2 |
| Command term | Calculate | Question number | 5 | Adapted from | N/A |
Question
A rocket of proper length 450 m is approaching a space station whose proper length is 9.0 km. The speed of the rocket relative to the space station is 0.80c.
X is an observer at rest in the space station.
Two lamps at opposite ends of the space station turn on at the same time according to X. Using a Lorentz transformation, determine, according to an observer at rest in the rocket,
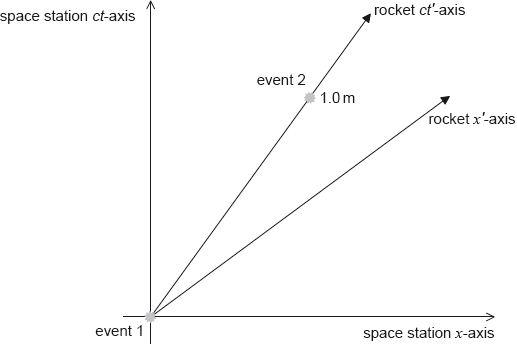
The rocket carries a different lamp. Event 1 is the flash of the rocket’s lamp occurring at the origin of both reference frames. Event 2 is the flash of the rocket’s lamp at time ct' = 1.0 m according to the rocket. The coordinates for event 2 for observers in the space station are x and ct.
Calculate the length of the rocket according to X.
A space shuttle is released from the rocket. The shuttle moves with speed 0.20c to the right according to X. Calculate the velocity of the shuttle relative to the rocket.
the time interval between the lamps turning on.
which lamp turns on first.
On the diagram label the coordinates x and ct.
State and explain whether the ct coordinate in (c)(i) is less than, equal to or greater than 1.0 m.
Calculate the value of c 2t 2 – x 2.
Markscheme
the gamma factor is \(\frac{5}{3}\) or 1.67
L = \(\frac{{450}}{{\frac{5}{3}}}\) = 270 «m»
Allow ECF from MP1 to MP2.
[2 marks]
u' = «\(\frac{{u - v}}{{1 - \frac{{uv}}{{{c^2}}}}} = \)» \(\frac{{0.20c - 0.80c}}{{1 - 0.20 \times 0.80}}\)
OR
0.2c = \( = \frac{{0.80c + u'}}{{1 + 0.80u'}}\)
u' = «–»0.71c
Check signs and values carefully.
[2 marks]
Δt' = «\(\gamma \left( {\Delta t - \frac{{v\Delta x}}{{{c^2}}}} \right) = \)» \(\frac{5}{3} \times \left( {0 - \frac{{\left( {0.80c \times 9000} \right)}}{{{c^2}}}} \right)\)
Δt' = «–»4.0 x 10–5 «s»
Allow ECF for use of wrong \(\gamma \) from (a)(i).
[2 marks]
lamp 2 turns on first
Ignore any explanation
[1 mark]
x coordinate as shown
ct coordinate as shown
Labels must be clear and unambiguous.
Construction lines are optional.
[2 marks]
«in any other frame» ct is greater
the interval ct' = 1.0 «m» is proper time
OR
ct is a dilated time
OR
ct = \(\gamma \)ct' «= \(\gamma \)»
MP1 is a statement
MP2 is an explanation
[2 marks]
use of c 2t 2 – x 2 = c 2t' 2 – x' 2
c 2t 2 – x 2 = 12 – 02 = 1 «m2»
for MP1 equation must be used.
Award [2] for correct answer that first finds x (1.33 m) and ct (1.66 m)
[2 marks]

