| Date | May 2018 | Marks available | 2 | Reference code | 18M.3.SL.TZ1.5 |
| Level | Standard level | Paper | Paper 3 | Time zone | Time zone 1 |
| Command term | Explain | Question number | 5 | Adapted from | N/A |
Question
An observer on Earth watches rocket A travel away from Earth at a speed of 0.80c. The spacetime diagram shows the worldline of rocket A in the frame of reference of the Earth observer who is at rest at x = 0.
Another rocket, B, departs from the same location as A but later than A at ct = 1.2 km according to the Earth observer. Rocket B travels at a constant speed of 0.60c in the opposite direction to A according to the Earth observer.
Rocket A and rocket B both emit a flash of light that are received simultaneously by the Earth observer. Rocket A emits the flash of light at a time coordinate ct = 1.8 km according to the Earth observer.
Draw on the spacetime diagram the worldline of B according to the Earth observer and label it B.
Deduce, showing your working on the spacetime diagram, the value of ct according to the Earth observer at which the rocket B emitted its flash of light.
Explain whether or not the arrival times of the two flashes in the Earth frame are simultaneous events in the frame of rocket A.
Calculate the velocity of rocket B relative to rocket A.
Markscheme
straight line with negative gradient with vertical intercept at ct = 1.2 «km»
through (–0.6, 2.2) ie gradient = –1.67
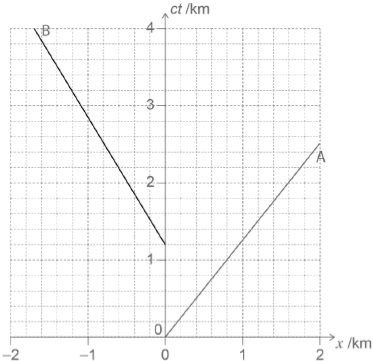
Tolerance: Allow gradient from interval –2.0 to –1.4, (at ct = 2.2, x from interval 0.5 to 0.7).
If line has positive gradient from interval 1.4 to 2.0 and intercepts at ct = 1.2 km then allow [1 max].
[2 marks]
line for the flash of light from A correctly drawn
line for the flash of light of B correctly drawn
correct reading taken for time of intersection of flash of light and path of B, ct = 2.4 «km»
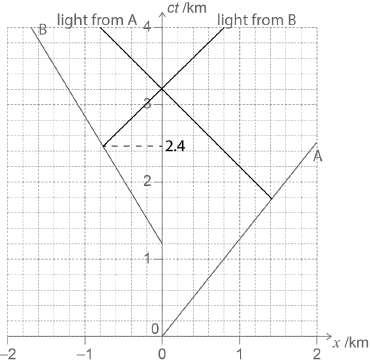
Accept values in the range: 2.2 to 2.6.
[3 marks]
the two events take place in the same point in space at the same time
so all observers will observe the two events to be simultaneous / so zero difference
Award the second MP only if the first MP is awarded.
[2 marks]
\(u' = \frac{{ - 0.6 - 0.8}}{{1 - ( - 0.6) \times 0.8}}\)
= «–»0.95 «c»
[2 marks]

