| Date | May 2017 | Marks available | 1 | Reference code | 17M.3.SL.TZ1.4 |
| Level | Standard level | Paper | Paper 3 | Time zone | Time zone 1 |
| Command term | Show that and Apply | Question number | 4 | Adapted from | N/A |
Question
An observer P sitting in a train moving at a speed v measures that his journey takes a time ΔtP. An observer Q at rest with respect to the ground measures that the journey takes a time ΔtQ.
According to Q there is an instant at which the train is completely within the tunnel.
At that instant two lights at the front and the back of the train are turned on simultaneously according to Q.
The spacetime diagram according to observer Q shows event B (back light turns on) and event F (front light turns on).
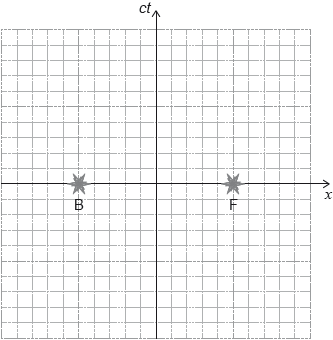
State which of the two time intervals is a proper time.
Calculate the speed v of the train for the ratio \(\frac{{\Delta {t_{\text{P}}}}}{{\Delta {t_{\text{Q}}}}} = 0.30\).
Later the train is travelling at a speed of 0.60c. Observer P measures the length of the train to be 125 m. The train enters a tunnel of length 100 m according to observer Q.
Show that the length of the train according to observer Q is 100 m.
Draw the time \(ct'\) and space \(x'\) axes for observer P’s reference frame on the spacetime diagram.
Deduce, using the spacetime diagram, which light was turned on first according to observer P.
Apply a Lorentz transformation to show that the time difference between events B and F according to observer P is 2.5 × 10–7 s.
Demonstrate that the spacetime interval between events B and F is invariant.
A second train is moving at a velocity of –0.70c with respect to the ground.
Calculate the speed of the second train relative to observer P.
Markscheme
ΔtP / observer sitting in the train
[1 mark]
\(\gamma = \frac{{\Delta {t_{\text{Q}}}}}{{\Delta {t_{\text{P}}}}} = \) «\( = \frac{1}{{0.30}}\)» = 3.3
to give v = 0.95c
[2 marks]
\(\gamma \) = 1.25
«length of train according Q» = 125/1.25
«giving 100m»
[2 marks]
axes drawn with correct gradients of \(\frac{5}{3}\) for \(ct'\) and 0.6 for \(x'\)
Award [1] for one gradient correct and another approximately correct.
[1 mark]
lines parallel to the \(x'\) axis and passing through B and F
intersections on the \(ct'\) axis at \({\text{B'}}\) and \({\text{F'}}\) shown
light at the front of the train must have been turned on first
[3 marks]
\(\Delta t' = 1.25 \times \frac{{0.6 \times 100}}{{3 \times {{10}^8}}}\)
«2.5 × 10−7»
Allow ECF for gamma from (c).
[1 mark]
according to P: \({\left( {3 \times {{10}^8} \times 2.5 \times {{10}^{ - 7}}} \right)^2} - {125^2} = \) «−» 10000
according to Q: \({\left( {3 \times {{10}^8} \times 0} \right)^2} - {100^2} = \) «−» 10000
[2 marks]
\(u' = \frac{{ - 0.7 - 0.6}}{{1 + 0.7 \times 0.6}}\) c
= «−» 0.92c
[2 marks]

