| Date | May 2013 | Marks available | 2 | Reference code | 13M.2.hl.TZ1.3 |
| Level | HL | Paper | 2 | Time zone | TZ1 |
| Command term | Determine | Question number | 3 | Adapted from | N/A |
Question
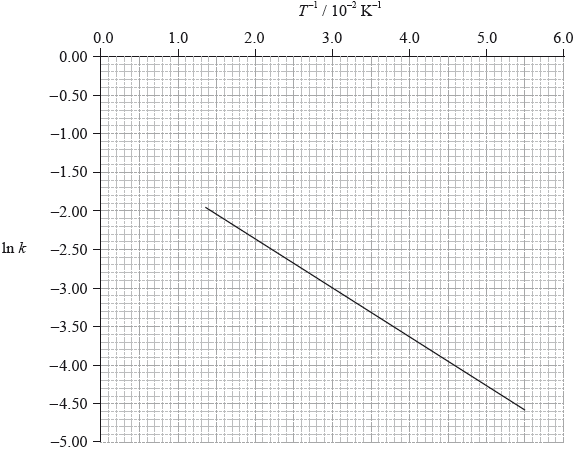
To determine the activation energy of a reaction, the rate of reaction was measured at different temperatures. The rate constant, \(k\), was determined and \(\ln k\) was plotted against the inverse of the temperature in Kelvin, \({T^{ - 1}}\). The following graph was obtained.
Define the term activation energy, \({E_{\text{a}}}\).
Use the graph on page 8 to determine the value of the activation energy, \({E_{\text{a}}}\), in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\).
On the graph on page 8, sketch the line you would expect if a catalyst is added to the reactants.
Markscheme
minimum energy needed to react/start a reaction / energy difference between reactants and transition state;
gradient of the line: –63;
Accept –60 to –65.
\({E_{\text{a}}}{\text{ }}( = - R \times {\text{gradient}}) = 0.52{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
Accept 0.50 to 0.54.
gradient of the line less steep (less negative);
Accept any position as long as gradient less steep.
Examiners report
The idea of activation energy being a minimum was seldom communicated. Few were able to follow through all the mathematics to find \({E_{\text{a}}}\) by a graphical method and those that did had often omitted \({\text{1}}{{\text{0}}^{ - 2}}\) in their calculations. The answers were often poorly set out so it was difficult to assess the award of part marks; indeed, many candidates seemed to hope that a correct answer would somehow emerge from a mass of incomprehensible figures.
The idea of activation energy being a minimum was seldom communicated. Few were able to follow through all the mathematics to find \({E_{\text{a}}}\) by a graphical method and those that did had often omitted \({\text{1}}{{\text{0}}^{ - 2}}\) in their calculations. The answers were often poorly set out so it was difficult to assess the award of part marks; indeed, many candidates seemed to hope that a correct answer would somehow emerge from a mass of incomprehensible figures.
The idea of activation energy being a minimum was seldom communicated. Few were able to follow through all the mathematics to find \({E_{\text{a}}}\) by a graphical method and those that did had often omitted \({\text{1}}{{\text{0}}^{ - 2}}\) in their calculations. The answers were often poorly set out so it was difficult to assess the award of part marks; indeed, many candidates seemed to hope that a correct answer would somehow emerge from a mass of incomprehensible figures. The gradient of the graph for (c) was generously marked; all candidates had to do was to realize that the catalyst would lower the activation energy and thus the gradient would be less negative. As long as a line with less negative gradient was drawn, the mark was awarded.

