| Date | May 2011 | Marks available | 1 | Reference code | 11M.2.hl.TZ1.2 |
| Level | HL | Paper | 2 | Time zone | TZ1 |
| Command term | State | Question number | 2 | Adapted from | N/A |
Question
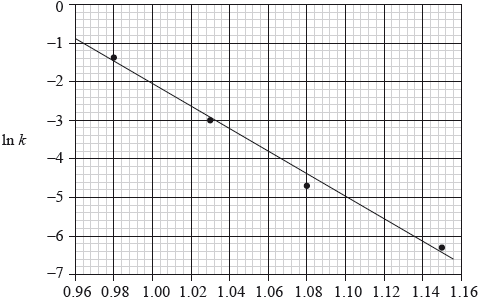
Consider the following graph of \(\ln k\) against \(\frac{1}{T}\) (temperature in Kelvin) for the second order decomposition of \({{\text{N}}_{\text{2}}}{\text{O}}\) into \({{\text{N}}_{\text{2}}}\) and O.
\[{{\text{N}}_{\text{2}}}{\text{O}} \to {{\text{N}}_{\text{2}}} + {\text{O}}\]
\[\frac{1}{T}/{10^{ - 3}}{\text{ }}{{\text{K}}^{ - 1}}\]
State how the rate constant, \(k\) varies with temperature,\(T\).
Determine the activation energy, \({E_{\text{a}}}\), for this reaction.
The rate expression for this reaction is rate \( = k{{\text{[}}{{\text{N}}_{\text{2}}}{\text{O]}}^{\text{2}}}\) and the rate constant is \({\text{0.244 d}}{{\text{m}}^{\text{3}}}{\text{mo}}{{\text{l}}^{ - 1}}{{\text{s}}^{ - 1}}\) at 750 °C.
A sample of \({{\text{N}}_{\text{2}}}{\text{O}}\) of concentration \({\text{0.200 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) is allowed to decompose. Calculate the rate when 10% of the \({{\text{N}}_{\text{2}}}{\text{O}}\) has reacted.
Markscheme
\(k\) increases with increase in \(T/k\) decreases with decrease in \(T\);
Do not allow answers giving just the Arrhenius equation or involving lnk relationships.
\({\text{gradient}} = - {E_{\text{a}}}/R\);
\( - 30000{\text{ }}(K) = - {E_{\text{a}}}/R\);
Allow value in range –28800–31300 (K).
\(0.9 \times 0.200 = 0.180{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
\({\text{rate}} = \left( {0.244 \times {{(0.180)}^2} = } \right){\text{ }}7.91 \times {10^{ - 3}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{{\text{s}}^{ - 1}}\);
Award [2] for correct final answer.
Award [1 max] for either 9.76 \( \times \) 10–3 mol\(\,\)dm–3s–1 or 9.76 \( \times \) 10–5 mol\(\,\)dm–3s–1.
Examiners report
This question on chemical kinetics was very poorly answered by candidates. In (a), many candidates simply gave the Arrhenius equation and failed to describe the explicit relationship between \(k\) and \(T\).
(b) was answered very poorly and although some candidates had an idea about the gradient expression, most were out by a factor of 100 in their final answer and many totally ignored units.
In (c), the most common error related to the 10% reduction and units also proved challenging.

