| Date | November 2013 | Marks available | 2 | Reference code | 13N.2.hl.TZ0.1 |
| Level | HL | Paper | 2 | Time zone | TZ0 |
| Command term | State | Question number | 1 | Adapted from | N/A |
Question
Reaction kinetics can be investigated using the iodine clock reaction. The equations for two reactions that occur are given below.
Reaction A: \({{\text{H}}_2}{{\text{O}}_2}{\text{(aq)}} + {\text{2}}{{\text{I}}^ - }{\text{(aq)}} + {\text{2}}{{\text{H}}^ + }{\text{(aq)}} \to {{\text{I}}_2}{\text{(aq)}} + {\text{2}}{{\text{H}}_2}{\text{O(l)}}\)
Reaction B: \({\text{ }}{{\text{I}}_2}{\text{(aq)}} + {\text{2}}{{\text{S}}_2}{\text{O}}_3^{2 - }{\text{(aq)}} \to {\text{2}}{{\text{I}}^ - }{\text{(aq)}} + {{\text{S}}_4}{\text{O}}_6^{2 - }{\text{(aq)}}\)
Reaction B is much faster than reaction A, so the iodine, \({\text{I}_2}\), formed in reaction A immediately reacts with thiosulfate ions, \({{\text{S}}_{\text{2}}}{\text{O}}_3^{2 - }\), in reaction B, before it can react with starch to form the familiar blue-black, starch-iodine complex.
In one experiment the reaction mixture contained:
5.0 ± 0.1 \({\text{c}}{{\text{m}}^{\text{3}}}\) of 2.00 \({\text{mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) hydrogen peroxide (\({{\text{H}}_{\text{2}}}{{\text{O}}_{\text{2}}}\))
5.0 ± 0.1 \({\text{c}}{{\text{m}}^{\text{3}}}\) of 1% aqueous starch
20.0 ± 0.1 \({\text{c}}{{\text{m}}^{\text{3}}}\) of 1.00 \({\text{mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sulfuric acid (\({{\text{H}}_{\text{2}}}{\text{S}}{{\text{O}}_{\text{4}}}\))
20.0 ± 0.1 \({\text{c}}{{\text{m}}^{\text{3}}}\) of 0.0100 \({\text{mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) sodium thiosulfate (\({\text{N}}{{\text{a}}_{\text{2}}}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{3}}}\))
50.0 ± 0.1 \({\text{c}}{{\text{m}}^{\text{3}}}\) of water with 0.0200 ± 0.0001 g of potassium iodide (KI) dissolved in it.
After 45 seconds this mixture suddenly changed from colourless to blue-black.
The activation energy can be determined using the Arrhenius equation, which is given in Table 1 of the Data Booklet. The experiment was carried out at five different temperatures. An incomplete graph to determine the activation energy of the reaction, based on these results, is shown below.
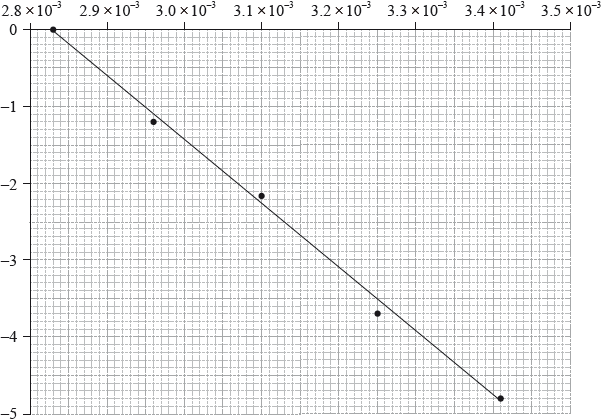
The concentration of iodide ions, \({{\text{I}}^ - }\), is assumed to be constant. Outline why this is a valid assumption.
For this mixture the concentration of hydrogen peroxide, \({{\text{H}}_{\text{2}}}{{\text{O}}_{\text{2}}}\), can also be assumed to be constant. Explain why this is a valid assumption.
Explain why the solution suddenly changes colour.
Calculate the total uncertainty, in \({\text{c}}{{\text{m}}^{\text{3}}}\), of the volume of the reaction mixture.
Calculate the percentage uncertainty of the concentration of potassium iodide solution added to the overall reaction mixture.
Determine the percentage uncertainty in the concentration of potassium iodide in the final reaction solution.
The colour change occurs when \(1.00 \times {10^{ - 4}}{\text{ mol}}\) of iodine has been formed. Use the total volume of the solution and the time taken, to calculate the rate of the reaction, including appropriate units.
State the labels for each axis.
x-axis:
y-axis:
Use the graph to determine the activation energy of the reaction, in \({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}\), correct to three significant figures.
In another experiment, 0.100 g of a black powder was also added while all other concentrations and volumes remained unchanged. The time taken for the solution to change colour was now 20 seconds. Outline why you think the colour change occurred more rapidly and how you could confirm your hypothesis.
Markscheme
KI/\({{\text{I}}^ - }\)/potassium iodide/iodide (ion) (rapidly) reformed (in second stage of reaction);
amount (in mol) of \({{\text{H}}_{\text{2}}}{{\text{O}}_{\text{2}}}\)/hydrogen peroxide \( \gg \) amount (in mol) \({\text{N}}{{\text{a}}_{\text{2}}}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{3}}}{\text{/}}{{\text{S}}_{\text{2}}}{\text{O}}_3^{2 - }\)/sodium thiosulfate/ thiosulfate (ion);
Accept amount (in mol) of H2O2/hydrogen peroxide \( \gg \) amount (in mol) KI/I–/potassium iodide/iodide (ion).
Accept “H2O2/hydrogen peroxide is in (large) excess/high concentration”.
(at end of reaction) \({\text{[}}{{\text{H}}_{\text{2}}}{{\text{O}}_{\text{2}}}{\text{]}}\) is only slightly decreased/virtually unchanged;
all \({\text{N}}{{\text{a}}_{\text{2}}}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{3}}}\)/sodium thiosulfate/\({{\text{S}}_{\text{2}}}{\text{O}}_3^{2 - }\)/thiosulfate consumed/used up;
Accept “iodine no longer converted to iodide”.
(free) iodine is formed / iodine reacts with starch / forms iodine-starch complex;
\((5 \times 0.1) = ( \pm )0.5{\text{ }}({\text{c}}{{\text{m}}^{\text{3}}})\);
\(( \pm )0.7(\% )\);
Comprises both mass of KI = ± 0.5% and volume of KI = ± 0.2%.
\(0.5 + 0.7 = ( \pm )1.2\% \);
Sum of (i) and (ii) (percentage uncertainty of total volume = absolute uncertainty as 100 cm3).
total volume \(0.100{\text{ }}({\text{d}}{{\text{m}}^3})/100{\text{ }}({\text{c}}{{\text{m}}^3})\);
\(\left( {{\text{change in concentration }} = \frac{{{\text{1.00}} \times {\text{1}}{{\text{0}}^{ - 4}}}}{{{\text{0.100}}}} = } \right){\text{ 1.00}} \times {\text{1}}{{\text{0}}^{ - 3}}{\text{ (mol}}\,{\text{d}}{{\text{m}}^{\text{3}}}{\text{)}}\);
\(\left( {{\text{rate}} = \frac{{1.00 \times {{10}^{ - 3}}}}{{45}} = } \right){\text{ }}2.2 \times {10^{ - 5}}\);
Award [3] for the correct final answer.
\({\text{mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{{\text{s}}^{ - 1}}\);
x-axis: \(\frac{1}{{{\text{Temperature}}}}/\frac{1}{T}/{{\text{T}}^{ - 1}}\);
Ignore units.
y-axis: ln rate/\({\log _{\text{e}}}\) rate / ln rate constant/\({\log _{\text{e}}}\) rate constant / ln k/\({\log _{\text{e}}}k\);
gradient \( = \frac{{ - {E_{\text{a}}}}}{R}\);
gradient \( = \frac{{ - 4.00}}{{(3.31 \times {{10}^{ - 3}} - 2.83 \times {{10}^{ - 3}})}} = - 8333/ = \frac{{ - 4.80}}{{(3.41 \times {{10}^{ - 3}} - 2.83 \times {{10}^{ - 3}})}} = - 8276\);
\({E_{\text{a}}} = \left( {\frac{{8.31 \times 8333}}{{1000}}} \right) = 69.3{\text{ }}({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}})/ = \left( {\frac{{8.31 \times 8276}}{{1000}}} \right) = 68.8{\text{ }}({\text{kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}})\);
Award [3] for correct final answer.
Accept values from 65.0 to 73.0 kJ mol–1.
Deduct [1] for final answer in J mol–1.
Deduct [1] for final answer not to 3 significant figures.
acting as a catalyst / black powder reacts with thiosulfate ions / solid dissolves to give blue-black solution;
Accept any other valid suggestion which will make colour change more rapid.
For catalyst: amount/mass of black powder remains constant / no new/different products formed / activation energy decreased;
For other suggestions: any appropriate way to test the hypothesis;
Award [1] for valid hypothesis, [1] for appropriate method of testing the stated hypothesis.
Examiners report
This question explored basic chemical concepts in the context of a practical situation. Whilst this is one frequently carried out during practical courses, none of the questions depended on prior knowledge. Students varied significantly in their ability to interpret the information given to answer parts (a) to (c), but very few could correctly carry out the propagation of uncertainties required in part (d). An encouraging number were able to carry out the rate calculation required in part (e). It was surprising how many students, though unable to identify the axes of the Arrhenius graph given in part (f), were still able to interpret it to correctly calculate the activation energy. Part (g) was deliberately open ended and elicited a number of interesting responses, though frequently the tests proposed would not in fact confirm the suggested hypothesis.
This question explored basic chemical concepts in the context of a practical situation. Whilst this is one frequently carried out during practical courses, none of the questions depended on prior knowledge. Students varied significantly in their ability to interpret the information given to answer parts (a) to (c), but very few could correctly carry out the propagation of uncertainties required in part (d). An encouraging number were able to carry out the rate calculation required in part (e). It was surprising how many students, though unable to identify the axes of the Arrhenius graph given in part (f), were still able to interpret it to correctly calculate the activation energy. Part (g) was deliberately open ended and elicited a number of interesting responses, though frequently the tests proposed would not in fact confirm the suggested hypothesis.
This question explored basic chemical concepts in the context of a practical situation. Whilst this is one frequently carried out during practical courses, none of the questions depended on prior knowledge. Students varied significantly in their ability to interpret the information given to answer parts (a) to (c), but very few could correctly carry out the propagation of uncertainties required in part (d). An encouraging number were able to carry out the rate calculation required in part (e). It was surprising how many students, though unable to identify the axes of the Arrhenius graph given in part (f), were still able to interpret it to correctly calculate the activation energy. Part (g) was deliberately open ended and elicited a number of interesting responses, though frequently the tests proposed would not in fact confirm the suggested hypothesis.
This question explored basic chemical concepts in the context of a practical situation. Whilst this is one frequently carried out during practical courses, none of the questions depended on prior knowledge. Students varied significantly in their ability to interpret the information given to answer parts (a) to (c), but very few could correctly carry out the propagation of uncertainties required in part (d). An encouraging number were able to carry out the rate calculation required in part (e). It was surprising how many students, though unable to identify the axes of the Arrhenius graph given in part (f), were still able to interpret it to correctly calculate the activation energy. Part (g) was deliberately open ended and elicited a number of interesting responses, though frequently the tests proposed would not in fact confirm the suggested hypothesis.
This question explored basic chemical concepts in the context of a practical situation. Whilst this is one frequently carried out during practical courses, none of the questions depended on prior knowledge. Students varied significantly in their ability to interpret the information given to answer parts (a) to (c), but very few could correctly carry out the propagation of uncertainties required in part (d). An encouraging number were able to carry out the rate calculation required in part (e). It was surprising how many students, though unable to identify the axes of the Arrhenius graph given in part (f), were still able to interpret it to correctly calculate the activation energy. Part (g) was deliberately open ended and elicited a number of interesting responses, though frequently the tests proposed would not in fact confirm the suggested hypothesis.
This question explored basic chemical concepts in the context of a practical situation. Whilst this is one frequently carried out during practical courses, none of the questions depended on prior knowledge. Students varied significantly in their ability to interpret the information given to answer parts (a) to (c), but very few could correctly carry out the propagation of uncertainties required in part (d). An encouraging number were able to carry out the rate calculation required in part (e). It was surprising how many students, though unable to identify the axes of the Arrhenius graph given in part (f), were still able to interpret it to correctly calculate the activation energy. Part (g) was deliberately open ended and elicited a number of interesting responses, though frequently the tests proposed would not in fact confirm the suggested hypothesis.
This question explored basic chemical concepts in the context of a practical situation. Whilst this is one frequently carried out during practical courses, none of the questions depended on prior knowledge. Students varied significantly in their ability to interpret the information given to answer parts (a) to (c), but very few could correctly carry out the propagation of uncertainties required in part (d). An encouraging number were able to carry out the rate calculation required in part (e). It was surprising how many students, though unable to identify the axes of the Arrhenius graph given in part (f), were still able to interpret it to correctly calculate the activation energy. Part (g) was deliberately open ended and elicited a number of interesting responses, though frequently the tests proposed would not in fact confirm the suggested hypothesis.
This question explored basic chemical concepts in the context of a practical situation. Whilst this is one frequently carried out during practical courses, none of the questions depended on prior knowledge. Students varied significantly in their ability to interpret the information given to answer parts (a) to (c), but very few could correctly carry out the propagation of uncertainties required in part (d). An encouraging number were able to carry out the rate calculation required in part (e). It was surprising how many students, though unable to identify the axes of the Arrhenius graph given in part (f), were still able to interpret it to correctly calculate the activation energy. Part (g) was deliberately open ended and elicited a number of interesting responses, though frequently the tests proposed would not in fact confirm the suggested hypothesis.
This question explored basic chemical concepts in the context of a practical situation. Whilst this is one frequently carried out during practical courses, none of the questions depended on prior knowledge. Students varied significantly in their ability to interpret the information given to answer parts (a) to (c), but very few could correctly carry out the propagation of uncertainties required in part (d). An encouraging number were able to carry out the rate calculation required in part (e). It was surprising how many students, though unable to identify the axes of the Arrhenius graph given in part (f), were still able to interpret it to correctly calculate the activation energy. Part (g) was deliberately open ended and elicited a number of interesting responses, though frequently the tests proposed would not in fact confirm the suggested hypothesis.
This question explored basic chemical concepts in the context of a practical situation. Whilst this is one frequently carried out during practical courses, none of the questions depended on prior knowledge. Students varied significantly in their ability to interpret the information given to answer parts (a) to (c), but very few could correctly carry out the propagation of uncertainties required in part (d). An encouraging number were able to carry out the rate calculation required in part (e). It was surprising how many students, though unable to identify the axes of the Arrhenius graph given in part (f), were still able to interpret it to correctly calculate the activation energy. Part (g) was deliberately open ended and elicited a number of interesting responses, though frequently the tests proposed would not in fact confirm the suggested hypothesis.

