| Date | November 2011 | Marks available | 1 | Reference code | 11N.2.hl.TZ0.5 |
| Level | HL | Paper | 2 | Time zone | TZ0 |
| Command term | Estimate | Question number | 5 | Adapted from | N/A |
Question
Consider the reaction:
\[{\text{CuS(s)}} + {{\text{H}}_2}{\text{(g)}} \to {\text{Cu(s)}} + {{\text{H}}_2}{\text{S(g)}}\]
Given:
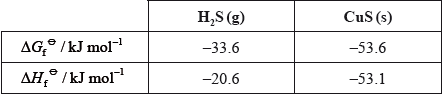
Deduce and explain the sign of the entropy change for the following reaction.
\[{\text{CO(g)}} + {\text{2}}{{\text{H}}_{\text{2}}}{\text{(g)}} \to {\text{C}}{{\text{H}}_{\text{3}}}{\text{OH(l)}}\]
Suggest why the \(\Delta H_{\text{f}}^\Theta \) values for \({{\text{H}}_{\text{2}}}{\text{(g)}}\) and Cu(s) are not given in the table.
Determine the standard enthalpy change at 298 K for the reaction.
Determine the standard free energy change at 298 K for the reaction. Deduce whether or not the reaction is spontaneous at this temperature.
Determine the standard entropy change at 298 K for the reaction.
Estimate the temperature, in K, at which the standard change in free energy equals zero. You should assume that the values of the standard enthalpy and entropy changes are not affected by the change in temperature.
Markscheme
negative;
liquid more ordered than gaseous phase or vice-versa / OWTTE;
\(\Delta H_{\text{f}}^\Theta \) of an element (in its most stable state) is zero (since formation of an element from itself is not a reaction) / OWTTE;
Do not allow an answer such as because they are elements.
\(\Delta {H^\Theta }( = (1)( - 20.6) - (1)( - 53.1)) = 32.5{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}/32500{\text{ (J}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
Allow 32.5 (kJ) or 3.25 \( \times \) 104 (J).
\(\Delta {G^\Theta }( = (1)( - 33.6) - (1)( - 53.6)) = 20.0{\text{ (kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}/20000{\text{ (J}}\,{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
Allow 20.0 (kJ) or 2.00 \( \times \) 104 (J).
non-spontaneous;
\(\Delta {S^\Theta }( = (\Delta {H^\Theta } - \Delta {G^\Theta })/T = (32.5 - 20.0)(1000)/298) = 41.9{\text{ (J}}\,{{\text{K}}^{ - 1}}{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}/\)
\(4.19 \times {10^{ - 2}}{\text{ (kJ}}\,{{\text{K}}^{ - 1}}{\text{mo}}{{\text{l}}^{ - 1}}{\text{)}}\);
Allow 41.9 (J\(\,\)K–1) or 4.19 \( \times \) 10–2 (kJ\(\,\)K–1).
\(T{\text{ }}\left( { = \Delta H/\Delta S = (32.5 \times 1000)/(41.9)} \right) = 776{\text{ (K)}}\);
Examiners report
The negative nature of the change gained a mark, but the explanations sometimes lacked clarity and states often were not referred to.
In (i), often there was no mention of element.
(ii) to (iv) was often very well done, though as usual some candidates struggled with units.
(ii) to (iv) was often very well done, though as usual some candidates struggled with units.
(ii) to (iv) was often very well done, though as usual some candidates struggled with units.

