| Date | May 2008 | Marks available | 6 | Reference code | 08M.1.hl.TZ0.4 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
The triangle ABC is isosceles and AB = BC = 5. D is the midpoint of AC and BD = 4.
Find the lengths of the tangents from A, B and D to the circle inscribed in the triangle ABD.
Markscheme
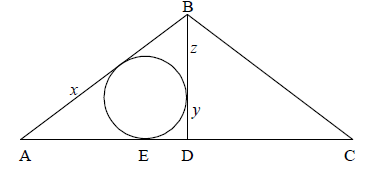
AD \( = 3\) (A1)
Let the lengths of the tangents be as shown.
Then,
\(x + y = 3\)
\(y + z = 4\)
\(x + z = 5\) (M1)A1
Solving,
\(x = 2\) , \(y = 1\) , \(z = 3\) A1A1A1
[6 marks]
Examiners report
[N/A]

