| Date | May 2010 | Marks available | 2 | Reference code | 10M.1.hl.TZ0.6 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Show that | Question number | 6 | Adapted from | N/A |
Question
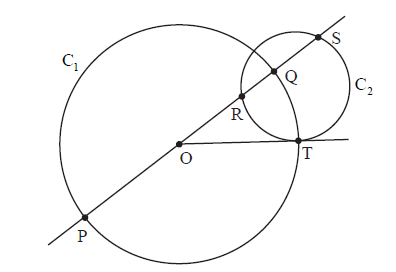
The figure shows a circle C1 with centre O and diameter [PQ] and a circle C2 which intersects (PQ) at the points R and S. T is one point of intersection of the two circles and (OT) is a tangent to C2 .
Show that \(\frac{{{\rm{OR}}}}{{{\rm{OT}}}} = \frac{{{\rm{OT}}}}{{{\rm{OS}}}}\) .
(i) Show that \({\rm{PR}} - {\rm{RQ}} = 2{\rm{OR}}\) .
(ii) Show that \(\frac{{{\rm{PR}} - {\rm{RQ}}}}{{{\rm{PR}} + {\rm{RQ}}}} = \frac{{{\rm{PS}} - {\rm{SQ}}}}{{{\rm{PS}} + {\rm{SQ}}}}\) .
Markscheme
by the tangent – secant theorem, M1
\({\rm{O}}{{\rm{T}}^2} = {\rm{OR}} \bullet {\rm{OS}}\) A1
so that \(\frac{{{\rm{OR}}}}{{{\rm{OT}}}} = \frac{{{\rm{OT}}}}{{{\rm{OS}}}}\) AG
[2 marks]
(i) \({\rm{PR}} - {\rm{RQ}} = {\rm{PO}} + {\rm{OR}} - ({\rm{OQ}} - {\rm{OR}})\) A1
\( = 2{\rm{OR}}\) AG
(ii) attempt to continue the process set up in (b)(i) (M1)
\({\rm{PR + RQ}} = {\rm{PO}} + {\rm{OR + OQ}} - {\rm{OR}} = 2{\rm{OT}}\) A1
\({\rm{PS}} - {\rm{SQ}} = {\rm{PQ}} + {\rm{QS}} - {\rm{SQ}} = 2{\rm{OT}}\) A1
\({\rm{PS + SQ}} = {\rm{PO}} + {\rm{OS}} - {\rm{OQ}} = 2{\rm{OS}}\) A1
it now follows that
\(\frac{{{\rm{PR}} - {\rm{RQ}}}}{{{\rm{PR}} + {\rm{RQ}}}} = \frac{{{\rm{OR}}}}{{{\rm{OT}}}}\) and \(\frac{{{\rm{PS}} - {\rm{SQ}}}}{{{\rm{PS}} + {\rm{SQ}}}} = \frac{{{\rm{OT}}}}{{{\rm{OS}}}}\) so using the result in part (a) R1
\(\frac{{{\rm{PR}} - {\rm{RQ}}}}{{{\rm{PR}} + {\rm{RQ}}}} = \frac{{{\rm{PS}} - {\rm{SQ}}}}{{{\rm{PS}} + {\rm{SQ}}}}\) AG
[6 marks]
Examiners report
Most candidates solved (a) correctly although some used similar triangles instead of the more obvious tangent-secant theorem.
Although (b) and then (c) were fairly well signposted, many candidates were unable to cope with the required algebra.

