| Date | May 2015 | Marks available | 3 | Reference code | 15M.1.hl.TZ0.13 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Explain | Question number | 13 | Adapted from | N/A |
Question
Two line segments [\(\rm{AB}\)] and [\(\rm{CD}\)] meet internally at the point \(\rm{Y}\). Given that
\({\text{YA}} \times {\text{YB}} = {\text{YC}} \times {\text{YD }}\) show that \(\rm{A}\), \(\rm{B}\), \(\rm{C}\) and \(\rm{D}\) all lie on the circumference of a circle.
Explain why the result also holds if the line segments meet externally at \(\rm{Y}\).
Markscheme
METHOD 1
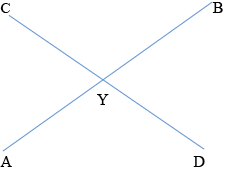
Consider the triangles \(\rm{ACY}\) and \(\rm{DBY}\) M1
Then \({\text{YA}} \times {\text{YB}} = {\text{YC}} \times {\text{YD }}\)
It follows that \(\frac{{{\text{YA}}}}{{{\text{YD}}}} = \frac{{{\text{YC}}}}{{{\text{YB}}}}\) A1
Also \({\rm{A\hat YC}} = {\rm{D\hat YB}}\) A1
The triangles \(\rm{ACY}\) and \(\rm{DBY}\) are therefore similar A1
So \({\rm{A\hat CY}} = {\rm{D\hat BY}}\) A1
Therefore by the converse to the angles subtended by a chord theorem,
the points \(\rm{A}\), \(\rm{B}\), \(\rm{C}\), \(\rm{D}\) lie on a circle. R1
METHOD 2
consider the circle passing through \(\rm{ABC}\) M1
the circle then cuts the line \((\rm{CD})\) at \(\rm{K}\) M1
Note: May be seen on diagram
since \(\rm{Y}\) lies inside the circle, \(\rm{Y}\) divides the chord \(\rm{CK}\) internally
hence \(\rm{K}\) and \(\rm{D}\) are on the same side of \(\rm{Y}\) (R1)
\({\text{YA}} \times {\text{YB}} = {\text{YC}} \times {\text{YK}}\) since \(\rm{A}\), \(\rm{B}\), \(\rm{C}\) and \(\rm{K}\) are concyclic M1
\({\text{YA}} \times {\text{YB}} = {\text{YC}} \times {\text{YD }}\) given
\( \Rightarrow {\text{YC}} \times {\text{YK}} = {\text{YC}} \times {\text{YD }}\) A1
hence \(\rm{K}\) and \(\rm{D}\) are the same point R1
the circle passes through \(\rm{D}\)
Note: Allow an argument based on similar triangles and angles in the segment
Do not allow the use of the converse of the intersecting chords theorem in either (a) or (b)
METHOD 1
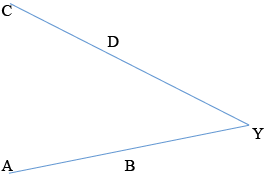
Since the triangles \(\rm{ACY}\) and \(\rm{DBY}\) are still similar \({\rm{A\hat CY}} = {\rm{D\hat BY}}\) A1
Therefore \({\rm{A\hat CY}} + {\rm{D\hat BA}} = {\rm{A\hat CY}} + 180^\circ - {\rm{D\hat BY}}\)
\( = 180^\circ \) A1
\(\rm{ACDB}\) is therefore a cyclic quadrilateral so the points \(\rm{A}\), \(\rm{B}\), \(\rm{C}\), \(\rm{D}\) lie on a circle. R1
METHOD 2
again consider the circle passing through \(\rm{ABC}\) and again let it cut the line \(\rm{CD}\) at \(\rm{K}\). M1
in this case \(\rm{Y}\) lies outside the circle \(\rm{ABC}\) and therefore \(\rm{Y}\) divides the chord \(\rm{CK}\) externally. M1
by the secant-secant theorem the same working applies as in part (a) R1
and the proof follows identically. AG
Examiners report
Many candidates made no significant attempt at this question. It was expected that solutions would use the intersecting chords theorem but in the event, the majority of candidates who answered the question used similar triangles successfully to prove the required result.
Many candidates made no significant attempt at this question. It was expected that solutions would use the intersecting chords theorem but in the event, the majority of candidates who answered the question used similar triangles successfully to prove the required result.

