| Date | May 2009 | Marks available | 8 | Reference code | 09M.2.hl.TZ0.5 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Prove that | Question number | 5 | Adapted from | N/A |
Question
Prove that the interior bisectors of two of the angles of a non-isosceles triangle and the exterior bisector of the third angle, meet the sides of the triangle in three collinear points.
An equilateral triangle QRT is inscribed in a circle. If S is any point on the arc QR of the circle,
(i) prove that \({\rm{ST}} = {\rm{SQ}} + {\rm{SR}}\) ;
(ii) show that triangle RST is similar to triangle PSQ where P is the intersection of [TS] and [QR];
(iii) using your results from parts (i) and (ii) deduce that \(\frac{1}{{{\rm{SP}}}} = \frac{1}{{{\rm{SQ}}}} + \frac{1}{{{\rm{SR}}}}\) .
Perpendiculars are drawn from a point P on the circumcircle of triangle LMN to the three sides. The perpendiculars meet the sides [LM], [MN] and [LN] at the points E, F and G respectively.
Prove that \({\rm{PL}} \times {\rm{PF}} = {\rm{PM}} \times {\rm{PG}}\) .
Markscheme
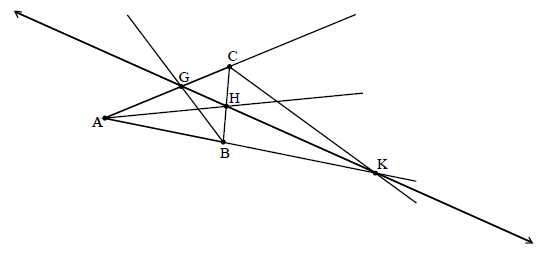
triangle ABC has interior angle bisectors AH, BG and exterior angle bisector CK
using the angle bisector theorem, M1
\(\frac{{{\rm{CH}}}}{{{\rm{HB}}}} = \frac{{{\rm{CA}}}}{{{\rm{AB}}}}\) , \(\frac{{{\rm{AG}}}}{{{\rm{GC}}}} = \frac{{{\rm{AB}}}}{{{\rm{CB}}}}\) , \(\frac{{{\rm{BK}}}}{{{\rm{AK}}}} = \frac{{{\rm{CB}}}}{{{\rm{CA}}}}\) A2
hence, \(\frac{{{\rm{CH}}}}{{{\rm{HB}}}} \times \frac{{{\rm{AG}}}}{{{\rm{GC}}}} \times \frac{{{\rm{BK}}}}{{{\rm{AK}}}} = \frac{{{\rm{CA}}}}{{{\rm{AB}}}} \times \frac{{{\rm{AB}}}}{{{\rm{CB}}}} \times \frac{{{\rm{CB}}}}{{{\rm{CA}}}} = 1\) M1A1
but \(\frac{{{\rm{BK}}}}{{{\rm{AK}}}} = - \frac{{{\rm{BK}}}}{{{\rm{KA}}}}\) R1
so, \(\frac{{{\rm{CH}}}}{{{\rm{HB}}}} \times \frac{{{\rm{AG}}}}{{{\rm{GC}}}} \times \frac{{{\rm{BK}}}}{{{\rm{AK}}}} = - 1\) A1
hence, by converse Menelaus’ theorem, G, H and K are collinear R1
[8 marks]
(i)
\({\rm{ST}} \bullet {\rm{QR}} = {\rm{SQ}} \bullet {\rm{RT}} + {\rm{SR}} \bullet {\rm{QT}}\) M1A1
but \({\rm{QT = QR = RT}}\) R1
hence \({\rm{ST = SQ + SR}}\) AG
(ii) \(\angle {\rm{STR = }}\angle {\rm{SQR}}\) R1
\(\angle {\rm{QST = }}\angle {\rm{QRT = }}{60^ \circ }\) A1
\(\angle {\rm{RST = }}\angle {\rm{RQT = }}{60^ \circ }\) A1
hence \(\angle {\rm{QST = }}\angle {\rm{RST}}\) and \(\Delta {\rm{RST}} \sim \Delta {\rm{PSQ}}\) R1
(iii) \(\frac{{{\rm{ST}}}}{{{\rm{SQ}}}} = \frac{{{\rm{SR}}}}{{{\rm{SP}}}} \to {\rm{ST}} \times {\rm{SP}} = {\rm{SR}} \times {\rm{SQ}}\) M1A1
but \({\rm{ST = (SQ + SR)}}\)
\({\rm{(SQ}} + {\rm{SR) \times SP}} = {\rm{SR}} \times {\rm{SQ}}\) A1
\({\rm{SQ}} \times {\rm{SP}} + {\rm{SR}} \times {\rm{SP}} = {\rm{SR}} \times {\rm{SQ}}\)
hence \(\frac{1}{{{\rm{SP}}}} = \frac{1}{{{\rm{SQ}}}} + \frac{1}{{{\rm{SR}}}}\) AG
[10 marks]
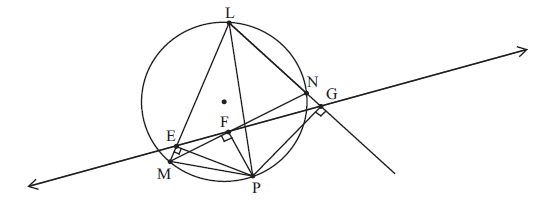
sine \(m\angle {\rm{PEM}} \cong m\angle {\rm{PFM}} \cong {90^ \circ }\)
then quadrilateral PFEM is cyclic M1A1
so \(m\angle {\rm{PME}} \cong m\angle {\rm{PFG}}\)
since \(m\angle {\rm{PGL}} \cong m\angle {\rm{PEL}} \cong {90^ \circ }\)
then quadrilateral PGLE is cyclic
so \(m\angle {\rm{PGE}} \cong m\angle {\rm{PLE}}\) R1A1
now E, F and G are collinear since they are on the Simson line of \(\Delta {\rm{LMN}}\) R1
hence \(\Delta {\rm{PFG}} \sim \Delta {\rm{PML}}\) A1
so \(\frac{{{\rm{PL}}}}{{{\rm{PM}}}} = \frac{{{\rm{PG}}}}{{{\rm{PF}}}} \Rightarrow {\rm{PL}} \times {\rm{PF}} = {\rm{PM}} \times {\rm{PG}}\) R1AG
[8 marks]
Examiners report
As in paper 1 there is a sad lack of knowledge of geometry although some good solutions were seen and at least one school is using techniques very successfully that are not mentioned in the program.
Part (a) was well done.
Few clear solutions to part (b) were seen.

