| Date | May 2014 | Marks available | 5 | Reference code | 14M.1.hl.TZ0.9 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Show that | Question number | 9 | Adapted from | N/A |
Question
\({\text{ABCDEF}}\) is a hexagon. A circle lies inside the hexagon and touches each of the six sides.
Show that \({\text{AB}} + {\text{CD}} + {\text{EF}} = {\text{BC}} + {\text{DE}} + {\text{FA}}\).
Markscheme
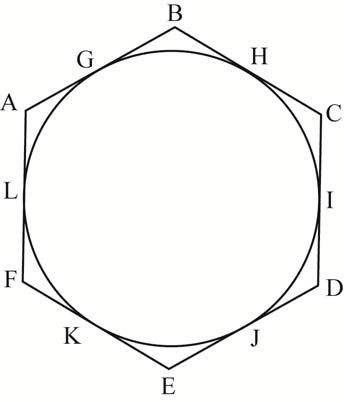 A1
A1
the lengths of the two tangents from a point to a circle are equal (R1)
so that
\({\text{AG}} = {\text{LA}}\)
\({\text{GB}} = {\text{BH}}\)
\({\text{CI}} = {\text{HC}}\)
\({\text{ID}} = {\text{DJ}}\)
\({\text{EK}} = {\text{JE}}\)
\({\text{KF}} = {\text{ FL}}\) A1
adding,
\({\text{(AG}} + {\text{GB)}} + {\text{(CI}} + {\text{ID)}} + {\text{(EK}} + {\text{KF)}} = {\text{(BH}} + {\text{HC)}} + {\text{(DJ}} + {\text{JE)}} + {\text{(FL}} + {\text{LA)}}\) M1A1
\({\text{AB}} + {\text{CD}} + {\text{EF}} = {\text{BC}} + {\text{DE}} + {\text{FA}}\) AG
[5 marks]

