| Date | May 2013 | Marks available | 3 | Reference code | 13M.2.hl.TZ0.6 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Show that | Question number | 6 | Adapted from | N/A |
Question
The circle \(C\) has centre O. The point Q is fixed in the plane of the circle and outside the circle. The point P is constrained to move on the circle.
Show that the opposite angles of a cyclic quadrilateral add up to \({180^ \circ }\) .
A quadrilateral ABCD is inscribed in a circle \(S\) . The four tangents to \(S\) at the vertices A, B, C and D form the edges of a quadrilateral EFGH. Given that EFGH is cyclic, show that AC and BD intersect at right angles.
Show that the locus of a point \({\rm{P'}}\) , which satisfies \(\overrightarrow {{\rm{QP'}}} = k\overrightarrow {{\rm{QP}}} \) , is a circle \(C'\) , where k is a constant and \(0 < k < 1\) .
Show that the two tangents to \(C\) from Q are also tangents to \({\rm{C'}}\) .
Markscheme
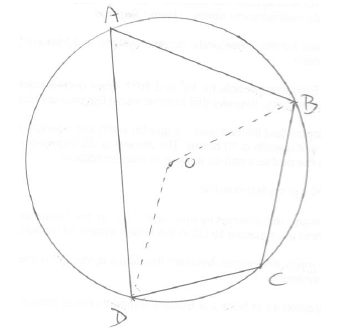
recognition of relevant theorem (M1)
eg \({\rm{D}}\hat {\rm{O}}{\rm{B}} = 2 \times {\rm{D}}\hat {\rm{A}}{\rm{B}}\) A1
\({360^ \circ } - {\rm{D}}\hat {\rm{O}}{\rm{B}} = 2 \times {\rm{D}}\hat {\rm{C}}{\rm{B}}\) A1
so \({\rm{D}}\hat {\rm{A}}{\rm{B}} + {\rm{D}}\hat {\rm{C}}{\rm{B}} = {\rm{18}}{0^ \circ }\) AG
[3 marks]
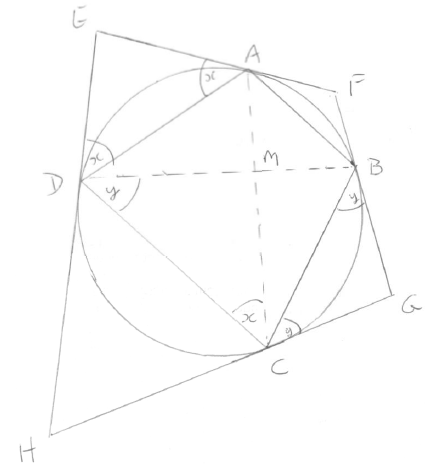
diagram showing tangents EAF, FBG, GCH and HDE; diagonals cross at M. M1
let \(x = {\rm{E}}\hat {\rm{D}}{\rm{A}} = {\rm{E}}\hat {\rm{A}}{\rm{D}}\) ; \(y = {\rm{B}}\hat {\rm{C}}{\rm{G}} = {\rm{C}}\hat {\rm{B}}{\rm{G}}\) A1
\({\rm{D}}\hat {\rm{E}}{\rm{A}} + {\rm{H}}\hat {\rm{G}}{\rm{F}} = 180 - 2x + 180 - 2y = 360 - 2(x + y)\) M1A1
\({\rm{C}}\hat {\rm{D}}{\rm{B}} = y\) and \({\rm{A}}\hat {\rm{C}}{\rm{D}} = x\) , as angles in alternate segments M1A1
\({\rm{D}}\hat {\rm{M}}{\rm{C}} = 180 - (x + y) = \left( {\frac{1}{2}} \right)({\rm{D}}\hat {\rm{E}}{\rm{A}} + {\rm{H}}\hat {\rm{G}}{\rm{F}}) = {90^ \circ }\) A1
so the diagonals cross at right angles AG
[7 marks]
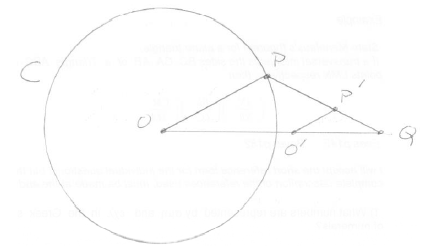
M1
let \({\rm{O'}}\) be the point on OQ such \({\rm{O'P'}}\) is parallel to OP A1
using similar triangles \({\rm{O'Q}} = k{\rm{OQ}}\) , so \({\rm{O'}}\) is a fixed point M1A1
and \({\rm{O'P}} = k{\rm{OP}}\) which is constant A1
so \({\rm{P'}}\) lies on a circle centre \({\rm{O'}}\) R1
so the locus of \({\rm{P'}}\) is a circle AG
[6 marks]
let one of the two tangents to \(C\) from Q touch \(C\) at T
the image of T lies on TQ A1
and is a unique point \({{\rm{T'}}}\) on \({C'}\) A1
so \({\rm{TT'}}\) is a common tangent and passes through Q R1
the same is true for the other tangent A1
so the two tangents to \(C\) from Q are also tangents to \({C'}\) AG
[4 marks]
Examiners report
(a) Most candidates produced a valid answer, although a small minority used a circular argument.
(b) A few candidates went straight to the core of this question. However, many other candidates produced incoherent answers containing some true statements, some irrelevancies and some incorrect statements, based on a messy diagram.
(a) This was poorly answered. Many candidates failed to note that the points Q, P and its image were defined to be collinear, and tried to invoke the notion of the Apollonius Circle theory. Others tried a coordinate approach – in principle this could work, but is actually quite tricky without a sensible choice of axes and the origin.

