| Date | May 2017 | Marks available | 1 | Reference code | 17M.2.sl.TZ2.1 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Show that | Question number | 1 | Adapted from | N/A |
Question
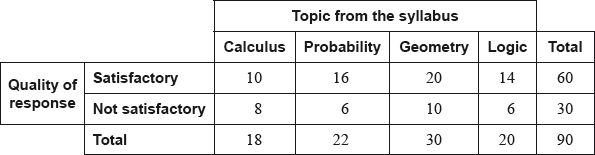
In a school, all Mathematical Studies SL students were given a test. The test contained four questions, each one on a different topic from the syllabus. The quality of each response was classified as satisfactory or not satisfactory. Each student answered only three of the four questions, each on a separate answer sheet.
The table below shows the number of satisfactory and not satisfactory responses for each question.
A \({\chi ^2}\) test is carried out at the 5% significance level for the data in the table.
The critical value for this test is 7.815.
If the teacher chooses a response at random, find the probability that it is a response to the Calculus question;
If the teacher chooses a response at random, find the probability that it is a satisfactory response to the Calculus question;
If the teacher chooses a response at random, find the probability that it is a satisfactory response, given that it is a response to the Calculus question.
The teacher groups the responses by topic, and chooses two responses to the Logic question. Find the probability that both are not satisfactory.
State the null hypothesis for this test.
Show that the expected frequency of satisfactory Calculus responses is 12.
Write down the number of degrees of freedom for this test.
Use your graphic display calculator to find the \({\chi ^2}\) statistic for this data.
State the conclusion of this \({\chi ^2}\) test. Give a reason for your answer.
Markscheme
\(\frac{1}{5}{\text{ }}\left( {\frac{{18}}{{90}};{\text{ }}0.2;{\text{ }}20\% } \right)\) (A1)(A1)(G2)
Note: Award (A1) for correct numerator, (A1) for correct denominator.
[2 marks]
\(\frac{1}{9}{\text{ }}\left( {\frac{{10}}{{90}};{\text{ }}0{\text{.}}\bar 1;{\text{ }}0.111111 \ldots ;{\text{ }}11.1\% } \right)\) (A1)(A1)(G2)
Note: Award (A1) for correct numerator, (A1) for correct denominator.
[2 marks]
\(\frac{5}{9}{\text{ }}\left( {\frac{{10}}{{18}};{\text{ }}0.\bar 5;{\text{ }}0.555556 \ldots ;{\text{ }}55.6\% } \right)\) (A1)(A1)(G2)
Note: Award (A1) for correct numerator, (A1) for correct denominator.
[2 marks]
\(\frac{6}{{20}} \times \frac{5}{{19}}\) (A1)(M1)
Note: Award (A1) for two correct fractions seen, (M1) for multiplying their two fractions.
\(\frac{3}{{38}}{\text{ }}\left( {\frac{{30}}{{380}};{\text{ }}0.0789473 \ldots ;{\text{ }}7.89\% } \right)\) (A1)(G2)
[3 marks]
\({{\text{H}}_0}\): quality (of response) and topic (from the syllabus) are independent (A1)
Note: Accept there is no association between quality (of response) and topic (from the syllabus). Do not accept “not related” or “not correlated” or “influenced”.
[1 mark]
\(\frac{{18}}{{90}} \times \frac{{60}}{{90}} \times 90\)\(\,\,\,\)OR\(\,\,\,\)\(\frac{{18 \times 60}}{{90}}\) (M1)
Note: Award (M1) for correct substitution in expected value formula.
\(( = ){\text{ }}12\) (AG)
Note: The conclusion, \(( = ){\text{ }}12\), must be seen for the (A1) to be awarded.
[1 mark]
3 (A1)
[1 mark]
\((\chi _{calc}^2 = ){\text{ }}1.46{\text{ }}(1.46\overline {36} ;{\text{ }}1.46363 \ldots )\) (G2)
[2 marks]
\(1.46 < 7.815\)\(\,\,\,\)OR\(\,\,\,\)\(0.690688 \ldots > 0.05\) (R1)
the null hypothesis is not rejected (A1)(ft)
OR
the quality of the response and the topic are independent (A1)(ft)
Note: Award (R1) for a correct comparison of either their \({\chi ^2}\) statistic to the \({\chi ^2}\) critical value or the correct \(p\)-value 0.690688… to the test level, award (A1)(ft) for the correct result from that comparison. Accept “\(\chi _{{\text{calc}}}^2 < \chi _{{\text{crit}}}^2\)” for the comparison, but only if their \(\chi _{{\text{calc}}}^2\) value is explicitly seen in part (f). Follow through from their answers to part (f) and part (c). Do not award (R0)(A1).
[2 marks]

