| Date | May 2014 | Marks available | 2 | Reference code | 14M.1.sl.TZ2.8 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 8 | Adapted from | N/A |
Question
A group of 100 students gave the following responses to the question of how they get to school.
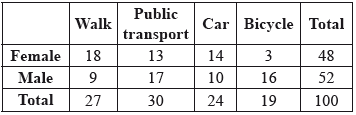
A \({\chi ^2}\) test for independence was conducted at the \(5\%\) significance level. The null hypothesis was defined as
\({{\text{H}}_0}\): Method of getting to school is independent of gender.
Find the expected frequency for the females who use public transport to get to school.
[2]
a.
Find the \({\chi ^2}\) statistic.
[2]
b.
The \({\chi ^2}\) critical value is \(7.815\) at the \(5\%\) significance level.
State whether or not the null hypothesis is accepted. Give a reason for your answer.
[2]
c.
Markscheme
\(\frac{{30}}{{100}} \times \frac{{48}}{{100}} \times 100\) OR \(\frac{{30 \times 48}}{{100}}\) (M1)
Note: Award (M1) for correct substitution into correct formula.
\( = 14.4{\text{ }}\left( {\frac{{72}}{5}} \right)\) (A1) (C2)
[2 marks]
a.
\(13.0{\text{ }}(12.9554…)\) (A2) (C2)
Note: Award (A1)(A0) for \(12.9\).
[2 marks]
b.
the null hypothesis is not accepted (A1)(ft)
\(\chi _{calc}^2 > \chi _{crit}^2\) OR \(13.0 > 7.82\) (R1)
OR
the null hypothesis is not accepted (A1)(ft)
p-value \({\text{(0.0047) (0.00473391}} \ldots {\text{)}} < 0.05\) (R1) (C2)
Notes: Follow through from their answer to part (b).
Do not award (A1)(ft)(R0).
[2 marks]
c.
Examiners report
[N/A]
a.
[N/A]
b.
[N/A]
c.
Syllabus sections
Topic 4 - Statistical applications » 4.4 » The \({\chi ^2}\) test for independence: formulation of null and alternative hypotheses; significance levels; contingency tables; expected frequencies; degrees of freedom; \(p\)-values.
Show 143 related questions
- 18M.2.sl.TZ2.3e: State a conclusion for this test. Justify your answer.
- 18M.2.sl.TZ2.3d.ii: For this test find the p-value.
- 18M.2.sl.TZ2.3d.i: For this test state the null hypothesis.
- 18M.2.sl.TZ2.3c: Given that P(W > k) = 0.225 , find the value of k.
- 18M.2.sl.TZ2.3b.ii: Find the value of q.
- 18M.2.sl.TZ2.3b.i: Sketch a normal curve to represent this probability.
- 18M.2.sl.TZ2.3a.ii: In a training session there are 40 basketball players. Find the expected number of players...
- 18M.2.sl.TZ2.3a.i: Find the probability that a basketball player has a weight that is less than 61 kg.
- 18M.2.sl.TZ1.2h: Two flights are chosen at random from those which were slightly delayed. Find the...
- 18M.2.sl.TZ1.2f: Write down the probability that this flight arrived on time.
- 18M.2.sl.TZ1.2d.ii: Write down the associated p-value.
- 18M.2.sl.TZ1.2d.i: Write down the χ2 statistic.
- 18M.2.sl.TZ1.2a: State the alternative hypothesis.
- 18M.2.sl.TZ1.2b: Calculate the expected frequency of flights travelling at most 500 km and arriving slightly...
- 17N.2.sl.TZ0.1g: State the result of the test. Give a reason for your answer.
- 17N.2.sl.TZ0.1f.ii: Write down the \({\chi ^2}\) statistic.
- 17N.2.sl.TZ0.1f.i: Write down the \(p\)-value for the test;
- 17N.2.sl.TZ0.1e.ii: Write down the number of degrees of freedom.
- 17N.2.sl.TZ0.1e.i: Write down the null hypothesis for this test;
- 17N.2.sl.TZ0.1d: Find the expected frequency of students choosing the Science category and obtaining 31 to 40...
- 17N.2.sl.TZ0.1c.ii: Use your graphic display calculator to estimate the standard deviation of \(N\).
- 17N.2.sl.TZ0.1c.i: Use your graphic display calculator to estimate the mean of \(N\);
- 17N.2.sl.TZ0.1b.ii: Write down, for \(N\), the mid-interval value of the modal class.
- 17N.2.sl.TZ0.1b.i: Write down, for \(N\), the modal class;
- 17N.2.sl.TZ0.1a: State whether \(N\) is a discrete or a continuous variable.
- 18M.2.sl.TZ1.2e: State, with a reason, whether you would reject the null hypothesis.
- 16M.1.sl.TZ2.7c: State the conclusion of the test. Give a reason for your answer.
- 16M.1.sl.TZ2.7b: A \({\chi ^{\,2}}\) test at the \(5\,\% \) significance level is used to determine whether TV...
- 16M.1.sl.TZ2.7a: A survey was conducted among a random sample of people about their favourite TV show. People...
- 16M.1.sl.TZ1.10d: From the travellers taking part in the survey, 285 were 61 years or older and 420 preferred...
- 16M.1.sl.TZ1.10c: The critical value of this \(\chi {\,^2}\) test is \(21.026\). Use this information to write...
- 16M.1.sl.TZ1.10b: Find the number of degrees of freedom.
- 16M.1.sl.TZ1.10a: The manager of a travel agency surveyed 1200 travellers. She wanted to find out whether there...
- 10M.1.sl.TZ1.10a: State the null hypothesis, H0, for this test.
- 10M.1.sl.TZ1.10c: Of the 400 people Tony interviewed, 220 were male and 180 were female. 80 of the people had...
- 10M.1.sl.TZ1.10d: Tony used a 5 % level of significance for his test and obtained a p-value of 0.0634 correct...
- 10M.1.sl.TZ1.10b: Write down the number of degrees of freedom.
- 10M.1.sl.TZ2.9d: State whether the type of coffee drunk is independent of gender. Give a reason for your answer.
- 10M.1.sl.TZ2.9a.i: Write down the null hypothesis.
- 10M.1.sl.TZ2.9b: Write down the number of degrees of freedom for this test.
- 10M.1.sl.TZ2.9c: Write down the critical value for this test.
- 10N.2.sl.TZ0.1B.a: Write down the null hypothesis, H0, for this test.
- 10N.2.sl.TZ0.1B.b: Write down the number of degrees of freedom for this test.
- 10N.2.sl.TZ0.1B.d: Show that the expected number of females that have more than 5 meals per day is 13, correct...
- 10N.2.sl.TZ0.1B.e: Use your graphic display calculator to find the \(\chi _{calc}^2\) for this data.
- 10N.2.sl.TZ0.1B.f: Decide whether H0 must be accepted. Justify your answer.
- 10N.2.sl.TZ0.1B.c: Write down the critical value for this test.
- 12N.2.sl.TZ0.4c: The manager of the store wants to determine whether the screen size is independent of gender....
- 12N.2.sl.TZ0.4e: The manager of the store wants to determine whether the screen size is independent of gender....
- 12N.2.sl.TZ0.4f: The manager of the store wants to determine whether the screen size is independent of gender....
- 12N.2.sl.TZ0.4g: The manager of the store wants to determine whether the screen size is independent of gender....
- 12N.2.sl.TZ0.4b: The manager of the store wants to determine whether the screen size is independent of gender....
- 12N.2.sl.TZ0.4d: The manager of the store wants to determine whether the screen size is independent of gender....
- 12M.2.sl.TZ1.2d: Write down the critical value of \(\chi ^2\), at the 5 % level of significance.
- 12M.2.sl.TZ1.2f: Determine whether H0 should be accepted. Justify your answer.
- 12M.2.sl.TZ1.2a: Write down the null hypothesis, H0, for this test.
- 12M.2.sl.TZ1.2b: Find the expected value of female footballers.
- 12M.2.sl.TZ1.2c: Write down the number of degrees of freedom.
- 12M.2.sl.TZ1.2e: Use your graphic display calculator to determine the \(\chi _{calc}^2\) value.
- 12M.1.sl.TZ2.8a: Write down the null hypothesis.
- 12M.1.sl.TZ2.8b: The colours of the cars were red, green, blue, black and silver. Find the number of degrees...
- 12M.1.sl.TZ2.8c: At the 5 % significance level the \(\chi_{calc}^2\) was found to be 8.73. Write down the...
- 11N.2.sl.TZ0.2c: Pam decides to test her belief using a Chi-squared test at the \(5\% \) level of...
- 11N.2.sl.TZ0.2d: Write down (i) the Chi-squared calculated value; (ii) the number of degrees of...
- 11N.2.sl.TZ0.2e: State, giving a reason, whether there is sufficient evidence at the \(5\% \) level of...
- 09N.2.sl.TZ0.4B, c, i: The calculated value of \({\chi ^2}\) is \(1.367\) and the critical value of \({\chi ^2}\) is...
- 09N.2.sl.TZ0.4B, a: Write down the total number of male students.
- 09N.2.sl.TZ0.4B, b: Show that the expected frequency for males, whose favourite car colour is blue, is 12.6.
- 09M.1.sl.TZ1.6a: Find the number of degrees of freedom for the \(\chi^2\) test.
- 09M.1.sl.TZ1.6b: Write down the null hypothesis for the \(\chi^2\) test.
- 09M.1.sl.TZ1.6d: The critical value for the \(\chi^2\) test at the 5% significance level is 12.59. The...
- 11M.2.sl.TZ1.2B.d: A \({\chi ^2}\) test at the \(5\% \) significance level was carried out to determine whether...
- 11M.2.sl.TZ1.2B.e: A \({\chi ^2}\) test at the \(5\% \) significance level was carried out to determine whether...
- 11M.2.sl.TZ1.2B.f: A \({\chi ^2}\) test at the \(5\% \) significance level was carried out to determine whether...
- 11M.2.sl.TZ1.2B.g: A \({\chi ^2}\) test at the \(5\% \) significance level was carried out to determine whether...
- 09M.2.sl.TZ2.2i, b: For the number of fertilized plants with height greater than 75 cm, show that the expected...
- 09M.2.sl.TZ2.2i, c: Write down the value of \(\chi_{calc}^2\).
- 09M.2.sl.TZ2.2i, a: Write down the null and alternative hypotheses for this test.
- 09M.2.sl.TZ2.2i, d: Write down the number of degrees of freedom.
- 09M.2.sl.TZ2.2i, f: Is the manufacturer’s claim justified? Give a reason for your answer.
- 11M.2.sl.TZ2.1A.d: Use your graphic display calculator to find the \({\chi ^2}\) test statistic for this data.
- 13M.2.sl.TZ1.1b: Write down the number of degrees of freedom.
- 13M.2.sl.TZ1.1c: Write down the critical value for the test.
- 13M.2.sl.TZ1.1e: Use your graphic display calculator to find for the data (i) the \(\chi^2\) calculated...
- 11M.2.sl.TZ2.1A.e: State whether Ludmila accepts the null hypothesis. Give a reason for your answer.
- 11M.2.sl.TZ2.1A.c: Find the expected frequency for the females studying Spanish.
- 11M.2.sl.TZ2.1A.b: Write down the number of degrees of freedom.
- 11M.2.sl.TZ2.1A.a: State Ludmila’s null hypothesis.
- 13M.2.sl.TZ1.1a: State the null hypothesis, H0, for the test.
- 13M.2.sl.TZ1.1d: Show that the expected number of Medium Yield crops using Fertilizer C is 17, correct to the...
- 13M.2.sl.TZ1.1f: State the conclusion of the test. Give a reason for your decision.
- 13M.1.sl.TZ2.6a: Write down the null hypothesis.
- 13M.1.sl.TZ2.6b: Find the number of degrees of freedom for this test.
- 13M.1.sl.TZ2.6c: Write down the critical value for this test.
- 13M.1.sl.TZ2.6d: State the conclusion of this test. Give a reason for your decision.
- 07M.1.sl.TZ0.8a: Write a suitable null hypothesis for a \(\chi^2\) test on this data.
- 07M.1.sl.TZ0.8b: Write down the value of \(\chi^2\) for this data.
- 07M.1.sl.TZ0.8c: The number of degrees of freedom is 4. Show how this value is calculated.
- 07M.1.sl.TZ0.8d: The critical value, at the 5% level of significance, is 9.488. What conclusion can be drawn...
- SPM.1.sl.TZ0.8a: Find the expected number of female volleyball players under this hypothesis.
- SPM.1.sl.TZ0.8b: Write down the \(p\)-value for the test.
- SPM.1.sl.TZ0.8c: State, with a reason, the conclusion of the test.
- 07N.2.sl.TZ0.4ii.a: Draw a table with 2 rows and 4 columns of data so that Manuel can perform a chi-squared test.
- 07N.2.sl.TZ0.4ii.c: Find the expected frequency for the number of females who had ‘Comedy’ as their most-watched...
- 07N.2.sl.TZ0.4ii.b: State Manuel’s null hypothesis and alternative hypothesis.
- 07N.2.sl.TZ0.4ii.d: Using your graphic display calculator, or otherwise, find the chi-squared statistic for...
- 07N.2.sl.TZ0.4ii.e: (i) State the number of degrees of freedom available for this calculation. (ii) State his...
- 08N.2.sl.TZ0.3a: Jorge applies a \({\chi ^2}\) test at the \(5\% \) level to investigate whether wearing a...
- 08M.1.sl.TZ1.5a: Write down the null hypothesis.
- 08M.1.sl.TZ1.5b: Write down the number of degrees of freedom.
- 08M.1.sl.TZ1.5c: Write down the chi-squared value.
- 08M.1.sl.TZ1.5d: State whether or not you will reject the null hypothesis, giving a clear reason for your answer.
- 08M.2.sl.TZ2.2i.c: The market research organization tests the survey data to determine whether the brand of...
- 08M.2.sl.TZ2.2i.d: The market research organization tests the survey data to determine whether the brand of...
- 08M.2.sl.TZ2.2i.e: The market research organization tests the survey data to determine whether the brand of...
- 08M.2.sl.TZ2.2i.f: The market research organization tests the survey data to determine whether the brand of...
- 08M.2.sl.TZ2.2i.g: The market research organization tests the survey data to determine whether the brand of...
- 09N.2.sl.TZ0.4B, c, ii: The calculated value of \({\chi ^2}\) is \(1.367\) and the critical value of \({\chi ^2}\) is...
- 09N.2.sl.TZ0.4B, c, iv: The calculated value of \({\chi ^2}\) is \(1.367\) and the critical value of \({\chi ^2}\) is...
- 10M.1.sl.TZ2.9a.ii: Write down the alternative hypothesis.
- 14M.1.sl.TZ2.8c: The \({\chi ^2}\) critical value is \(7.815\) at the \(5\%\) significance level. State...
- 14M.1.sl.TZ2.8a: Find the expected frequency for the females who use public transport to get to school.
- 13N.1.sl.TZ0.8d: The critical value, at the \(5\%\) significance level, is \(7.815\). State, giving a reason,...
- 13N.1.sl.TZ0.8a: Write down the null hypothesis for this test.
- 13N.1.sl.TZ0.8b: Write down the number of degrees of freedom.
- 13N.1.sl.TZ0.8c: Write down the value of \(\chi _{calc}^2\).
- 14M.1.sl.TZ1.4a: State the null hypothesis.
- 14M.1.sl.TZ1.4b: Write down the number of degrees of freedom.
- 14M.1.sl.TZ1.4c: Write down (i) the \({\chi ^2}\) statistic; (ii) the associated p-value.
- 14M.1.sl.TZ1.4d: State, giving a reason, whether the null hypothesis should be accepted.
- 15M.1.sl.TZ2.7a: Write down the null hypothesis for this test.
- 15M.1.sl.TZ2.7b: Write down the observed number of viewers who preferred Rumba and were older than 20 years old.
- 15M.1.sl.TZ2.7c: Use your graphic display calculator to find the \(p\)-value for this test.
- 15M.1.sl.TZ2.7d: The producer claims that the type of Latin dance a viewer preferred is independent of their...
- 15M.2.sl.TZ1.1a: State (i) \({{\text{H}}_0}\), the null hypothesis for the test; (ii) ...
- 15M.2.sl.TZ1.1d: Find (i) the \({\chi ^2}\) statistic; (ii) the associated \(p\)-value for the test.
- 15M.2.sl.TZ1.1e: Determine, giving a reason, whether \({{\text{H}}_0}\) should be accepted.
- 15M.2.sl.TZ1.1b: Write down the number of degrees of freedom.
- 15M.2.sl.TZ1.1c: Show that the expected frequency of those between the ages of 26 and 40 who oppose the...
- 14N.1.sl.TZ0.10d: Minta found that the calculated value of the \({\chi ^2}\) test was 3.576. The critical value...
- 14N.1.sl.TZ0.10a: State Minta’s null hypothesis.
- 14N.1.sl.TZ0.10b: State the number of degrees of freedom.
- 14N.1.sl.TZ0.10c: 150 students showed a preference for a smoothie. Calculate the expected number of female...
