| Date | May 2015 | Marks available | 2 | Reference code | 15M.2.sl.TZ1.1 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Show that | Question number | 1 | Adapted from | N/A |
Question
In a debate on voting, a survey was conducted. The survey asked people’s opinion on whether or not the minimum voting age should be reduced to 16 years of age. The results are shown as follows.
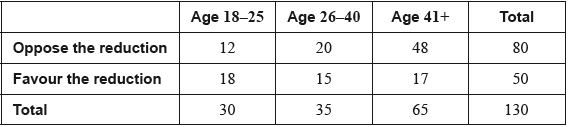
A \({\chi ^2}\) test at the 1% significance level was conducted. The \({\chi ^2}\) critical value of the test is 9.21.
State
(i) \({{\text{H}}_0}\), the null hypothesis for the test;
(ii) \({{\text{H}}_1}\), the alternative hypothesis for the test.
Write down the number of degrees of freedom.
Show that the expected frequency of those between the ages of 26 and 40 who oppose the reduction in the voting age is 21.5, correct to three significant figures.
Find
(i) the \({\chi ^2}\) statistic;
(ii) the associated \(p\)-value for the test.
Determine, giving a reason, whether \({{\text{H}}_0}\) should be accepted.
Markscheme
(i) \({{\text{H}}_0}\) age and opinion (about the reduction) are independent. (A1)
Notes: Accept “not associated” instead of independent.
(ii) \({{\text{H}}_1}\) age and opinion are not independent. (A1)(ft)
Notes: Follow through from part (a)(i). Accept “associated” or “dependent”.
Award (A1)(ft) for their correct \({{\text{H}}_1}\) worded consistently with their part (a)(i).
\(2\) (A1)
\(\frac{{80}}{{130}} \times \frac{{35}}{{130}} \times 130\;\;\;\)OR\(\;\;\;\frac{{80 \times 35}}{{130}}\) (M1)
Note: Award (M1) for \(\frac{{80}}{{130}} \times \frac{{35}}{{130}} \times 130\;\;\;\)OR\(\;\;\;\frac{{80 \times 35}}{{130}}\) seen. The following (A1) cannot be awarded without this statement.
\( = 21.5384 \ldots \) (A1)
\( = 21.5\) (AG)
Note: Both an unrounded answer that rounds to the given answer and rounded must be seen for the (A1) to be awarded. Accept \(21.54\) or \(21.53\) as an unrounded answer.
(i) \({\chi ^2}{\text{ statistic}} = 10.3\;\;\;(10.3257 \ldots )\) (G2)
Note: Accept \(10\) as a correct 2 significant figure answer.
(ii) \(p\)-value \( = 0.00573\;\;\;(0.00572531 \ldots )\) (G1)
since \(p\)-value \( < 0.01,{\text{ }}{{\text{H}}_0}\) should not be accepted (R1)(A1)(ft)
OR
since \({\chi ^2}{\text{ statistic}} > {\chi ^2}{\text{ critical value}},{\text{ }}{{\text{H}}_0}\) should not be accepted (R1)(A1)(ft)
Note: Do not award (R0)(A1). Follow through from their answer to part (d). Award (R0)(A0) if part (d) is unanswered.
Award (R1) for a correct comparison of either their \(p\)-value to the test level or their \({\chi ^2}\) statistic to the \({\chi ^2}\) critical value, award (A1) for the correct result from that comparison.
Examiners report
The great majority of candidates found this question to be a good start to the paper, with many perfect scores accruing. A common problem was the inability to form consistent null and alternative hypotheses. Also, calculating the expected value “by hand” as part of a “show that” question was left blank by a number of candidates; to reiterate again – to attain full marks, both the unrounded and the consistent and correctly rounded answer must be stated.
And, lastly, incorrect comparison of statistics when forming a conclusion was a common fault.
The great majority of candidates found this question to be a good start to the paper, with many perfect scores accruing. A common problem was the inability to form consistent null and alternative hypotheses. Also, calculating the expected value “by hand” as part of a “show that” question was left blank by a number of candidates; to reiterate again – to attain full marks, both the unrounded and the consistent and correctly rounded answer must be stated.
And, lastly, incorrect comparison of statistics when forming a conclusion was a common fault.
The great majority of candidates found this question to be a good start to the paper, with many perfect scores accruing. A common problem was the inability to form consistent null and alternative hypotheses. Also, calculating the expected value “by hand” as part of a “show that” question was left blank by a number of candidates; to reiterate again – to attain full marks, both the unrounded and the consistent and correctly rounded answer must be stated.
And, lastly, incorrect comparison of statistics when forming a conclusion was a common fault.
The great majority of candidates found this question to be a good start to the paper, with many perfect scores accruing. A common problem was the inability to form consistent null and alternative hypotheses. Also, calculating the expected value “by hand” as part of a “show that” question was left blank by a number of candidates; to reiterate again – to attain full marks, both the unrounded and the consistent and correctly rounded answer must be stated.
And, lastly, incorrect comparison of statistics when forming a conclusion was a common fault.
The great majority of candidates found this question to be a good start to the paper, with many perfect scores accruing. A common problem was the inability to form consistent null and alternative hypotheses. Also, calculating the expected value “by hand” as part of a “show that” question was left blank by a number of candidates; to reiterate again – to attain full marks, both the unrounded and the consistent and correctly rounded answer must be stated.
And, lastly, incorrect comparison of statistics when forming a conclusion was a common fault.

