| Date | May 2013 | Marks available | 4 | Reference code | 13M.1.sl.TZ1.2 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 2 | Adapted from | N/A |
Question
The diagram below shows part of the graph of \(f(x) = (x - 1)(x + 3)\) .
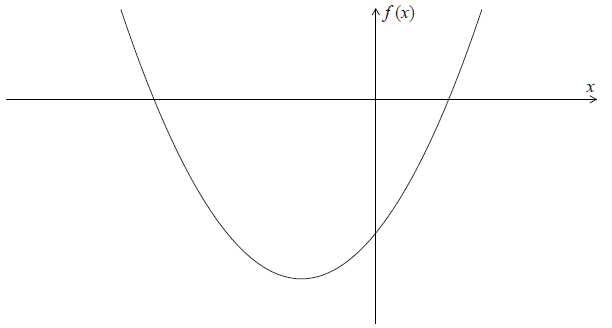
(a) Write down the \(x\)-intercepts of the graph of \(f\) .
(b) Find the coordinates of the vertex of the graph of \(f\) .
Write down the \(x\)-intercepts of the graph of \(f\) .
Find the coordinates of the vertex of the graph of \(f\) .
Markscheme
(a) \(x = 1\) , \(x = - 3\) (accept (\(1\), \(0\)), (\( - 3\), \(0\)) ) A1A1 N2
[2 marks]
(b) METHOD 1
attempt to find \(x\)-coordinate (M1)
eg \(\frac{{1 + - 3}}{2}\) , \(x = \frac{{ - b}}{{2a}}\) , \(f'(x) = 0\)
correct value, \(x = - 1\) (may be seen as a coordinate in the answer) A1
attempt to find their \(y\)-coordinate (M1)
eg \(f( - 1)\) , \( - 2 \times 2\) , \(y = \frac{{ - D}}{{4a}}\)
\(y = - 4\) A1
vertex (\( - 1\), \( - 4\)) N3
METHOD 2
attempt to complete the square (M1)
eg \({x^2} + 2x + 1 - 1 - 3\)
attempt to put into vertex form (M1)
eg \({(x + 1)^2} - 4\) , \({(x - 1)^2} + 4\)
vertex (\( - 1\), \( - 4\)) A1A1 N3
[4 marks]
\(x = 1\) , \(x = - 3\) (accept (\(1\), \(0\)), (\( - 3\), \(0\)) ) A1A1 N2
[2 marks]
METHOD 1
attempt to find \(x\)-coordinate (M1)
eg \(\frac{{1 + - 3}}{2}\) , \(x = \frac{{ - b}}{{2a}}\) , \(f'(x) = 0\)
correct value, \(x = - 1\) (may be seen as a coordinate in the answer) A1
attempt to find their \(y\)-coordinate (M1)
eg \(f( - 1)\) , \( - 2 \times 2\) , \(y = \frac{{ - D}}{{4a}}\)
\(y = - 4\) A1
vertex (\( - 1\), \( - 4\)) N3
METHOD 2
attempt to complete the square (M1)
eg \({x^2} + 2x + 1 - 1 - 3\)
attempt to put into vertex form (M1)
eg \({(x + 1)^2} - 4\) , \({(x - 1)^2} + 4\)
vertex (\( - 1\), \( - 4\)) A1A1 N3
[4 marks]
Examiners report
Most candidates recognized the values of the x-intercepts from the factorized form of the function. Candidates also showed little difficulty finding the vertex of the graph, and employed a variety of techniques: averaging \(x\)-intercepts, using \(x = \frac{{ - b}}{{2a}}\) , completing the square.
Most candidates recognized the values of the x-intercepts from the factorized form of the function. Candidates also showed little difficulty finding the vertex of the graph, and employed a variety of techniques: averaging \(x\)-intercepts, using \(x = \frac{{ - b}}{{2a}}\) , completing the square.
Most candidates recognized the values of the x-intercepts from the factorized form of the function. Candidates also showed little difficulty finding the vertex of the graph, and employed a variety of techniques: averaging \(x\)-intercepts, using \(x = \frac{{ - b}}{{2a}}\) , completing the square.

