| Date | November 2011 | Marks available | 1 | Reference code | 11N.1.sl.TZ0.1 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Write down | Question number | 1 | Adapted from | N/A |
Question
Let \(f\) be a quadratic function. Part of the graph of \(f\) is shown below.
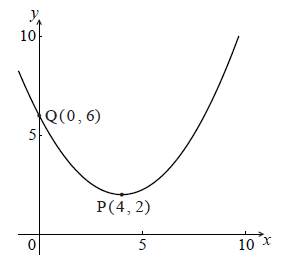
The vertex is at P(\(4\), \(2\)) and the y-intercept is at Q(\(0\), \(6\)) .
Write down the equation of the axis of symmetry.
The function f can be written in the form \(f(x) = a{(x - h)^2} + k\) .
Write down the value of h and of k .
The function f can be written in the form \(f(x) = a{(x - h)^2} + k\) .
Find a .
Markscheme
\(x = 4\) (must be an equation) A1 N1
[1 mark]
\(h = 4\) , \(k = 2\) A1A1 N2
[2 marks]
attempt to substitute coordinates of any point on the graph into f (M1)
e.g. \(f(0) = 6\) , \(6 = a{(0 - 4)^2} + 2\) , \(f(4) = 2\)
correct equation (do not accept an equation that results from \(f(4) = 2\) ) (A1)
e.g. \(6 = a{( - 4)^2} + 2\) , \(6 = 16a + 2\)
\(a = \frac{4}{{16}}\left( { = \frac{1}{4}} \right)\) A1 N2
[3 marks]
Examiners report
A surprising number of candidates missed part (a) of this question, which required them to write the equation of the axis of symmetry. Some candidates did not write their answer as an equation, while others simply wrote the formula \(x = - \frac{b}{{2a}}\) .
This was answered correctly by the large majority of candidates.
The rest of this question was answered correctly by the large majority of candidates. The mistakes seen in part (c) were generally due to either incorrect substitution of a point into the equation, or substitution of the vertex coordinates, which got the candidates nowhere.

