| Date | May 2008 | Marks available | 8 | Reference code | 08M.1.sl.TZ1.9 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find and Write down | Question number | 9 | Adapted from | N/A |
Question
Let \(f(x) = 3{(x + 1)^2} - 12\) .
Show that \(f(x) = 3{x^2} + 6x - 9\) .
For the graph of f
(i) write down the coordinates of the vertex;
(ii) write down the equation of the axis of symmetry;
(iii) write down the y-intercept;
(iv) find both x-intercepts.
Hence sketch the graph of f .
Let \(g(x) = {x^2}\) . The graph of f may be obtained from the graph of g by the two transformations:
a stretch of scale factor t in the y-direction
followed by a translation of \(\left( {\begin{array}{*{20}{c}}
p\\
q
\end{array}} \right)\) .
Find \(\left( {\begin{array}{*{20}{c}}
p\\
q
\end{array}} \right)\) and the value of t.
Markscheme
\(f(x) = 3({x^2} + 2x + 1) - 12\) A1
\( = 3{x^2} + 6x + 3 - 12\) A1
\( = 3{x^2} + 6x - 9\) AG N0
[2 marks]
(i) vertex is \(( - 1{\text{, }} - 12)\) A1A1 N2
(ii) \(x = - 1\) (must be an equation) A1 N1
(iii) \((0{\text{, }} - 9)\) A1 N1
(iv) evidence of solving \(f(x) = 0\) (M1)
e.g. factorizing, formula,
correct working A1
e.g. \(3(x + 3)(x - 1) = 0\) , \(x = \frac{{ - 6 \pm \sqrt {36 + 108} }}{6}\)
\(( - 3{\text{, }}0)\), \((1{\text{, }}0)\) A1A1 N1N1
[8 marks]
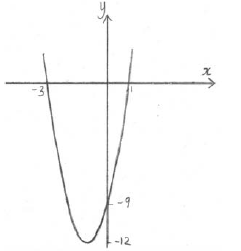 A1A1 N2
A1A1 N2
Note: Award A1 for a parabola opening upward, A1 for vertex and intercepts in approximately correct positions.
[2 marks]
\(\left( {\begin{array}{*{20}{c}}
p\\
q
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
{ - 1}\\
{ - 12}
\end{array}} \right)\) , \(t = 3\) (accept \(p = - 1\) , \(q = - 12\) , \(t = 3\) ) A1A1A1 N3
[3 marks]
Examiners report
This problem was generally well done. The “show that” question in part (a) was done correctly by most candidates, with a few attempting to show it by working backwards, which earned no marks.
Most candidates were able to identify the vertex but were unable to write the equation for the axis of symmetry. There was a great deal of success with the x and y intercepts.
Some of the sketches of the graph left much to be desired even if they were technically correct; many were v-shaped.
The final part was poorly done, indicating that defining a graph in terms of stretch and translation was unfamiliar to many candidates.

