| Date | May 2010 | Marks available | 1 | Reference code | 10M.1.sl.TZ2.1 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Write down | Question number | 1 | Adapted from | N/A |
Question
Let \(f(x) = p(x - q)(x - r)\) . Part of the graph of f is shown below.
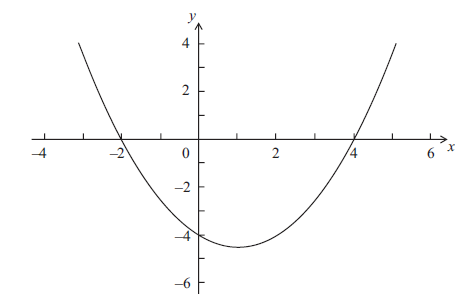
The graph passes through the points (−2, 0), (0, − 4) and (4, 0) .
Write down the value of q and of r.
Write down the equation of the axis of symmetry.
Find the value of p.
Markscheme
\(q = - 2\) , \(r = 4\) or \(q = 4\) , \(r = - 2\) A1A1 N2
[2 marks]
\(x = 1\) (must be an equation) A1 N1
[1 mark]
substituting \((0{\text{, }} - 4)\) into the equation (M1)
e.g. \( - 4 = p(0 - ( - 2))(0 - 4)\) , \( - 4 = p( - 4)(2)\)
correct working towards solution (A1)
e.g. \( - 4 = - 8p\)
\(p = \frac{4}{8}\) \(\left( { = \frac{1}{2}} \right)\) A1 N2
[3 marks]
Examiners report
The majority of candidates were successful on some or all parts of this question, with some candidates using a mix of algebra and graphical reasoning and others ignoring the graph and working only algebraically. Some did not recognize that p and q are the roots of the quadratic function and hence gave the answers as 2 and \( - 4\).
A common error in part (b) was the absence of an equation. Some candidates wrote down the equation \(x = \frac{{ - b}}{{2a}}\) but were not able to substitute correctly. Those students did not realize that the axis of symmetry is always halfway between the x-intercepts.
More candidates had trouble with part (c) with erroneous substitutions and simplification mistakes commonplace.

