| Date | None Specimen | Marks available | 7 | Reference code | SPNone.1.sl.TZ0.8 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find and Write down | Question number | 8 | Adapted from | N/A |
Question
Let \(f(x) = 3{(x + 1)^2} - 12\) .
Show that \(f(x) = 3{x^2} + 6x - 9\) .
For the graph of f
(i) write down the coordinates of the vertex;
(ii) write down the y-intercept;
(iii) find both x-intercepts.
Hence sketch the graph of f .
Let \(g(x) = {x^2}\) . The graph of f may be obtained from the graph of g by the following two transformations
a stretch of scale factor t in the y-direction,
followed by a translation of \(\left( \begin{array}{l}
p\\
q
\end{array} \right)\) .
Write down \(\left( \begin{array}{l}
p\\
q
\end{array} \right)\) and the value of t .
Markscheme
\(f(x) = 3({x^2} + 2x + 1) - 12\) A1
\( = 3{x^2} + 6x + 3 - 12\) A1
\( = 3{x^2} + 6x - 9\) AG N0
[2 marks]
(i) vertex is \(( - 1, - 12)\) A1A1 N2
(ii) \(y = - 9\) , or \((0, - 9)\) A1 N1
(iii) evidence of solving \(f(x) = 0\) M1
e.g. factorizing, formula
correct working A1
e.g. \(3(x + 3)(x - 1) = 0\) , \(x = \frac{{ - 6 \pm \sqrt {36 + 108} }}{6}\)
\(x = - 3\) , \(x = 1\) , or \(( - 3{\text{, }}0){\text{, }}(1{\text{, }}0)\) A1A1 N2
[7 marks]
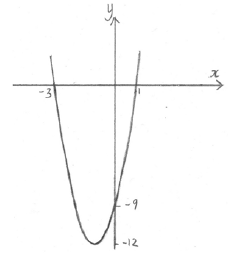A1A1A1 N3
Note: Award A1 for a parabola opening upward, A1 for vertex in approximately correct position, A1 for intercepts in approximately correct positions. Scale and labelling not required.
[3 marks]
\(\left( \begin{array}{l}
p\\
q
\end{array} \right) = \left( \begin{array}{l}
- 1\\
- 12
\end{array} \right)\) , \(t = 3\) A1A1A1 N3
[3 marks]
