| Date | May 2011 | Marks available | 2 | Reference code | 11M.2.sl.TZ1.10 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Show that | Question number | 10 | Adapted from | N/A |
Question
Let \(f(x) = {\log _3}\frac{x}{2} + {\log _3}16 - {\log _3}4\) , for \(x > 0\) .
Show that \(f(x) = {\log _3}2x\) .
Find the value of \(f(0.5)\) and of \(f(4.5)\) .
The function f can also be written in the form \(f(x) = \frac{{\ln ax}}{{\ln b}}\) .
(i) Write down the value of a and of b .
(ii) Hence on graph paper, sketch the graph of f , for \( - 5 \le x \le 5\) , \( - 5 \le y \le 5\) , using a scale of 1 cm to 1 unit on each axis.
(iii) Write down the equation of the asymptote.
Write down the value of \({f^{ - 1}}(0)\) .
The point A lies on the graph of f . At A, \(x = 4.5\) .
On your diagram, sketch the graph of \({f^{ - 1}}\) , noting clearly the image of point A.
Markscheme
combining 2 terms (A1)
e.g. \({\log _3}8x - {\log _3}4\) , \({\log _3}\frac{1}{2}x + {\log _3}4\)
expression which clearly leads to answer given A1
e.g. \({\log _3}\frac{{8x}}{4}\) , \({\log _3}\frac{{4x}}{2}\)
\(f(x) = {\log _3}2x\) AG N0
[2 marks]
attempt to substitute either value into f (M1)
e.g. \({\log _3}1\) , \({\log _3}9\)
\(f(0.5) = 0\) , \(f(4.5) = 2\) A1A1 N3
[3 marks]
(i) \(a = 2\) , \(b = 3\) A1A1 N1N1
(ii)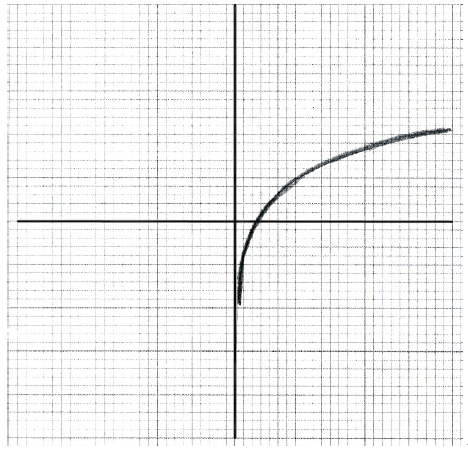 A1A1A1 N3
A1A1A1 N3
Note: Award A1 for sketch approximately through \((0.5 \pm 0.1{\text{, }}0 \pm 0.1)\) , A1 for approximately correct shape, A1 for sketch asymptotic to the y-axis.
(iii) \(x = 0\) (must be an equation) A1 N1
[6 marks]
\({f^{ - 1}}(0) = 0.5\) A1 N1
[1 mark]
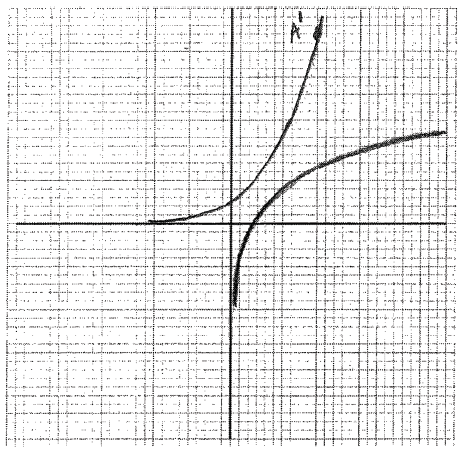 A1A1A1A1 N4
A1A1A1A1 N4
Note: Award A1 for sketch approximately through \((0 \pm 0.1{\text{, }}0.5 \pm 0.1)\) , A1 for approximately correct shape of the graph reflected over \(y = x\) , A1 for sketch asymptotic to x-axis, A1 for point \((2 \pm 0.1{\text{, }}4.5 \pm 0.1)\) clearly marked and on curve.
[4 marks]
Examiners report
Few candidates had difficulty with part (a) although it was often communicated using some very sloppy applications of the rules of logarithm, writing \(\frac{{\log 16}}{{\log 4}}\) instead of \(\log \left( {\frac{{16}}{4}} \right)\) .
Part (b) was generally done well.
Part (c) (i) was generally done well; candidates seemed quite comfortable changing bases. There were some very good sketches in (c) (ii), but there were also some very poor ones with candidates only considering shape and not the location of the x-intercept or the asymptote. A surprising number of candidates did not use the scale required by the question and/or did not use graph paper to sketch the graph. In some cases, it was evident that students simply transposed their graphs from their GDC without any analytical consideration.
Part (d) was poorly done as candidates did not consider the command term, “write down” and often proceeded to find the inverse function before making the appropriate substitution.
Part (e) eluded a great many candidates as most preferred to attempt to find the inverse analytically rather than simply reflecting the graph of f in the line \(y = x\) . This graph also suffered from the same sort of problems as the graph in (c) (ii). Some students did not have their curve passing through \((2{\text{, }}4.5)\) nor did they clearly indicate its position as instructed. This point was often mislabelled on the graph of f. The efforts in this question demonstrated that students often work tenuously from one question to the next, without considering the "big picture", thereby failing to make important links with earlier parts of the question.

