| Date | May 2016 | Marks available | 2 | Reference code | 16M.2.sl.TZ1.5 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | State | Question number | 5 | Adapted from | N/A |
Question
The mass \(M\) of a decaying substance is measured at one minute intervals. The points \((t,{\text{ }}\ln M)\) are plotted for \(0 \leqslant t \leqslant 10\), where \(t\) is in minutes. The line of best fit is drawn. This is shown in the following diagram.
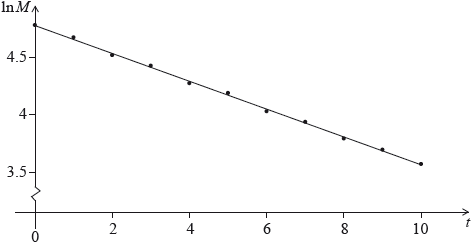
The correlation coefficient for this linear model is \(r = - 0.998\).
State two words that describe the linear correlation between \(\ln M\) and \(t\).
The equation of the line of best fit is \(\ln M = - 0.12t + 4.67\). Given that \(M = a \times {b^t}\), find the value of \(b\).
Markscheme
strong, negative (both required) A2 N2
[2 marks]
METHOD 1
valid approach (M1)
eg\(\,\,\,\,\,\)\({{\text{e}}^{\ln M}} = {{\text{e}}^{ - 0.12t + 4.67}}\)
correct use of exponent laws for \({{\text{e}}^{ - 0.12t + 4.67}}\) (A1)
eg\(\,\,\,\,\,\)\({{\text{e}}^{ - 0.12t}} \times {{\text{e}}^{4.67}}\)
comparing coefficients/terms (A1)
eg\(\,\,\,\,\,\)\({b^t} = {{\text{e}}^{ - 0.12t}}\)
\(b = {{\text{e}}^{ - 0.12}}{\text{ (exact), }}0.887\) A1 N3
METHOD 2
valid approach (M1)
eg\(\,\,\,\,\,\)\(\ln (a \times {b^t}) = - 0.12t + 4.67\)
correct use of log laws for \(\ln (a{b^t})\) (A1)
eg\(\,\,\,\,\,\)\(\ln a + t\ln b\)
comparing coefficients (A1)
eg\(\,\,\,\,\,\)\( - 0.12 = \ln b\)
\(b = {{\text{e}}^{ - 0.12}}{\text{ (exact), }}0.887\) A1 N3
[4 marks]
Examiners report
This turned out to be one of the more challenging questions on the paper. Although many candidates correctly described the linear correlation in part (a), a surprisingly large number of candidates were unable to do so.
Part (b) was not well done with many candidates unable to transfer their knowledge of exponentials and/or log manipulation to the question. After rewriting the line of best fit as \( = {{\text{e}}^{ - 0.12t + 4.67}}\), candidates were neither able to apply the rules for exponentials correctly nor were they familiar with the method of comparing coefficients to find the answer. There were numerous failed attempts of trying to estimate points from the graph and substitute these into the equation, while others arbitrarily chose values for \(t\) in an effort to set up a system of equations, the latter having some measure of success.

