| Date | May 2009 | Marks available | 2 | Reference code | 09M.1.sl.TZ2.9 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 9 | Adapted from | N/A |
Question
Two boxes contain numbered cards as shown below.
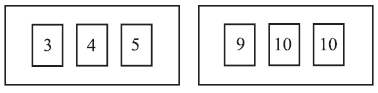
Two cards are drawn at random, one from each box.
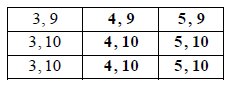
Copy and complete the table below to show all nine equally likely outcomes.

Let S be the sum of the numbers on the two cards.
Find the probability of each value of S.
Find the expected value of S.
Anna plays a game where she wins \(\$ 50\) if S is even and loses \(\$ 30\) if S is odd.
Anna plays the game 36 times. Find the amount she expects to have at the end of the 36 games.
Markscheme
 A2 N2
A2 N2
[2 marks]
\({\rm{P}}(12) = \frac{1}{9}\) , \({\rm{P}}(13) = \frac{3}{9}\) , \({\rm{P}}(14) = \frac{3}{9}\) , \({\rm{P}}(15) = \frac{2}{9}\) A2 N2
[2 marks]
correct substitution into formula for \({\text{E}}(X)\) A1
e.g. \({\rm{E}}(S) = 12 \times \frac{1}{9} + 13 \times \frac{3}{9} + 14 \times \frac{3}{9} + 15 \times \frac{2}{9}\)
\({\rm{E}}(S) = \frac{{123}}{9}\) A2 N2
[3 marks]
METHOD 1
correct expression for expected gain E(A) for 1 game (A1)
e.g. \(\frac{4}{9} \times 50 - \frac{5}{9} \times 30\)
\({\rm{E}}(A) = \frac{{50}}{9}\)
amount at end = expected gain for 1 game \( \times 36\) (M1)
= 200 (dollars) A1 N2
METHOD 2
attempt to find expected number of wins and losses (M1)
e.g. \(\frac{4}{9} \times 36\) , \(\frac{5}{9} \times 36\)
attempt to find expected gain E(G) (M1)
e.g. \(16 \times 50 - 30 \times 20\)
\({\text{E}}(G) = 200\) (dollars) A1 N2
[3 marks]
Examiners report
Most candidates completed parts (a), (b) and (c) successfully.
Most candidates completed part (b) successfully.
Many found the expected value correctly, while some showed difficulty with the arithmetic.
This was often left blank or only superficially attempted. Some found the expected value \(\frac{{50}}{9}\) but did not answer the question about the amount of money.

