| Date | May 2009 | Marks available | 1 | Reference code | 09M.1.sl.TZ1.2 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 2 | Adapted from | N/A |
Question
The letters of the word PROBABILITY are written on 11 cards as shown below.
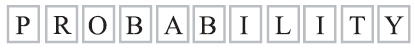
Two cards are drawn at random without replacement.
Let A be the event the first card drawn is the letter A.
Let B be the event the second card drawn is the letter B.
Find \({\rm{P}}(A)\) .
Find \({\rm{P}}(B|A)\) .
Find \({\rm{P}}(A \cap B)\) .
Markscheme
\({\rm{P}}(A) = \frac{1}{{11}}\) A1 N1
[1 mark]
\({\rm{P}}(B|A) = \frac{2}{{10}}\) A2 N2
[2 marks]
recognising that \({\rm{P}}(A \cap B) = {\rm{P}}(A) \times {\rm{P}}(B|A)\) (M1)
correct values (A1)
e.g. \({\rm{P}}(A \cap B) = \frac{1}{{11}} \times \frac{2}{{10}}\)
\({\rm{P}}(A \cap B) = \frac{2}{{110}}\) A1 N3
[3 marks]
Examiners report
Most candidates answered part (a) correctly.
Few candidates used the concept of "B given A" to simply "write down" the answer of \(\frac{2}{{10}}\) . Instead, most reached for the formula in the booklet, with which few were successful.
Few also made the connection that part (c) could be answered using both previous answers. Many found \({\rm{P}}(A \cap B)\) correctly even when answering part (b) incorrectly, although some candidates did not decrease the denominator for the second event.

