Problem of the Week #12  (29 August 2020)

SOLUTION

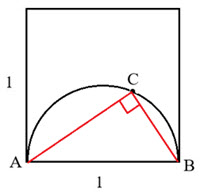(a)  Firstly, wherever point C is located, angle A and angle B of triangle ABC must both be acute angles. Hence, angle C must be obtuse for triangle ABC to be an obtuse triangle. Secondly, the probability of point C being inside a region where angle C is obtuse is the ratio of the area of that region to the area of the square. Since the area of the square is one, the probability of C lying in a particular region is the area of the region itself. Thirdly, an angle inscribed in a semicircle is a right angle (see figure). Hence, if C is in the semicircle then triangle ABC is obtuse. The area of the semicircle is \(\frac{1}{2}{\textrm{\pi }}{r^2} = \frac{1}{2}{\textrm{\pi }}{\left( {\frac{1}{2}} \right)^2} = \frac{{\textrm{\pi }}}{8}\). Therefore, if C is a randomly chosen point in the interior of the square then the probability that triangle ABC is obtuse is \(\frac{{\textrm{\pi }}}{8} \approx 0.393\)

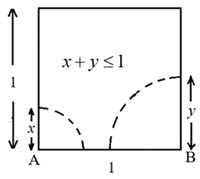(b)  For triangle ABC (\({\textrm{AC}} = x\), \({\textrm{BC}} = y\) and \({\textrm{AB}} = 1\)) to be obtuse, two conditions must be satisfied. Firstly, for the line segments with lengths of \(x\), \(y\) and 1 to form a triangle it must be that \(x + y > 1\). If \(x + y \le 1\), then the circle with centre at A and radius \(x\) will not intersect the circle with centre at B and radius \(y\). So, the first condition that must be met is \(x + y > 1\).

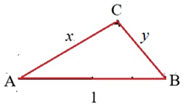
Secondly, triangle ABC must be obtuse; and, as explained in the solution for (b) above, this can only occur if angle C is obtuse. The cosine rule for triangle ABC gives \({1^2} = {x^2} + {y^2} - 2xy\cos C\) which can be rearranged to \({x^2} + {y^2} = 1 + 2xy\cos C\). If angle C is obtuse, then  must be negative. Hence, \({x^2} + {y^2} < 1\).

Thus, along with the conditions that \(0 < x < 1\) and \(0 < y < 1\), two further conditions to be satisfied for lengths \(x\), \(y\) and 1 to form an obtuse triangle are:

  (i) \(x + y > 1\), and  (ii) \({x^2} + {y^2} < 1\).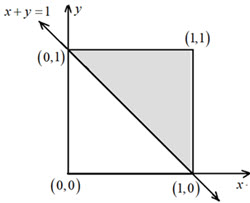

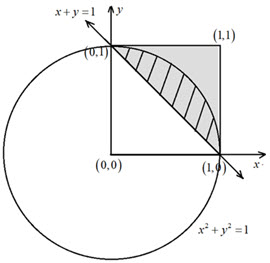
Given \(0 < x < 1\) and \(0 < y < 1\), \(x\) and \(y\) are the coordinates of a point inside a unit square with vertices at \(\left( {0,0} \right),\;\left( {1,0} \right),\;\left( {1,1} \right)\) and \(\left( {0,1} \right)\). The points in this square that also satisfy (i) \(x + y > 1\) are in the shaded triangle above the line \(x + y = 1\) (figure right). Points that satisfy (ii) \({x^2} + {y^2} < 1\) must lie in the unit circle with centre at \(\left( {0,0} \right)\). Thus, the set of points that satisfy all four conditions are in the region where the unit circle overlaps the shaded triangle. This region (a segment of the unit circle) is shown in the figure below; and its area is given by the area of the triangle with vertices \(\left( {0,0} \right),\;\left( {1,0} \right)\) and \(\left( {0,1} \right)\) subtracted from the quarter unit circle. Therefore, the probability that x, y and 1 are the sides of a obtuse triangle is \(\frac{1}{4}{\textrm{\pi }}\left( {{1^2}} \right) - \frac{1}{2}\left( 1 \right)\left( 1 \right) = \frac{{\textrm{\pi }}}{4} - \frac{1}{2} = \frac{{{\textrm{\pi }} - 2}}{4}\).