Problem of the Week #9   (31 May 2020)

SOLUTION

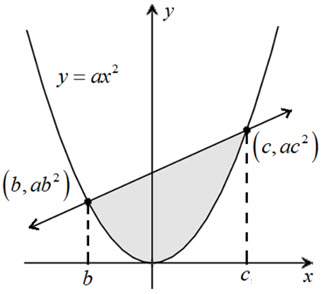
gradient of line, \(m = \frac{{a{c^2} - a{b^2}}}{{c - b}} = \frac{{a\left( {c + b} \right)\left( {c - b} \right)}}{{c - b}} = ac + ab\)

equation of line:  \(y - a{b^2} = \left( {ac + ab} \right)\left( {x - b} \right)\)

\(y = \left( {ac + ab} \right)x - abc - a{b^2} + a{b^2}\)

\(y = \left( {ac + ab} \right)x - abc\)

area of bounded region  \( = \int_b^c {\left\{ {\left[ {\left( {ac + ab} \right)x - abc} \right] - a{x^2}} \right\}} \,dx\)

\( = \int_b^c {\left\{ { - a{x^2} + \left( {ac + ab} \right)x - abc} \right\}dx} \)

\( = \left. { - \frac{1}{3}a{x^3} + \frac{1}{2}\left( {ac + ab} \right){x^2} - abcx} \right]_b^c\)

\( = \left[ { - \frac{1}{3}a{c^3} + \frac{1}{2}\left( {ac + ab} \right){c^2} - ab{c^2}} \right] - \left[ { - \frac{1}{3}a{b^3} + \frac{1}{2}\left( {ac + ab} \right){b^2} - a{b^2}c} \right]\)

\( = - \frac{1}{3}a{c^3} + \frac{1}{2}a{c^3} + \frac{1}{2}ab{c^2} - ab{c^2} + \frac{1}{3}a{b^3} - \frac{1}{2}a{b^3} - \frac{1}{2}a{b^2}c + a{b^2}c\)

\( = \frac{1}{6}a{c^3} - \frac{1}{6}a{b^3} - \frac{1}{2}ab{c^2} + \frac{1}{2}a{b^2}c\)

\( = \frac{a}{6}\left( {{c^3} - {b^3}} \right) - \frac{{abc}}{2}\left( {c - b} \right)\)

\( = \frac{a}{6}\left( {c - b} \right)\left( {{c^2} + bc + {b^2}} \right) - \frac{{abc}}{2}\left( {c - b} \right)\)

\( = \frac{a}{6}\left( {c - b} \right)\left[ {\left( {{c^2} + bc + {b^2}} \right) - 3bc} \right]\)

\( = \frac{a}{6}\left( {c - b} \right)\left( {{c^2} - 2bc + {b^2}} \right)\)

\( = \frac{a}{6}\left( {c - b} \right){\left( {c - b} \right)^2}\;\;\; \Rightarrow \;\;\;\)thus, area of bounded region \( = \frac{a}{6}{\left( {c - b} \right)^3}\)     Q.E.D.

Comment: For a given value of a, the area of the parabolic segment is determined by the value of \(c - b\). If the horizontal distance between the points of intersection is constant then the area of the parabolic segment will remain constant regardless of the location of the points of intersection.