Problem of the Week #8   (21 May 2020)

SOLUTION

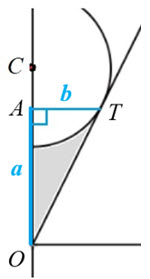
Consider the right triangle OAT where O is the origin and T is the point where the circle is tangent to the graph of \(y = k\left| x \right|\) such that \(OA = a\) and \(AT = b\). Because the slope of the right side of the graph of \(y = k\left| x \right|\) is \(k\), then \(\frac{a}{b} = \frac{k}{1}\).  Now consider right triangle CTO.  Triangles OAT and CTO are similar (corresponding sides proportional); so, \(\frac{a}{b} = \frac{k}{1} = \frac{{OT}}{{CT}}\). Since CT is a radius of the unit circle then \(\frac{k}{1} = \frac{{OT}}{1}\;\;\; \Rightarrow \;\;\;OT = k\). 

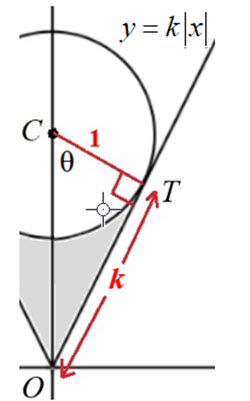
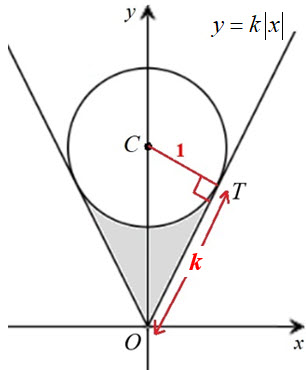
The area of the shaded region can be found by computing the area of triangle CTO and subtracting the sector of the unit circle with central angle \({\textrm{\theta }}\), as shown in the diagram; and then doubling this to get the area of the entire shaded region.

\({\textrm{\theta }} = \arctan \left( {\frac{k}{1}} \right) = \arctan \left( k \right)\);   area of sector \( = \frac{1}{2}{\textrm{\theta }}{r^2}\)

therefore, area of shaded region =

\( = 2\left[ {\frac{1}{2} \cdot k - \frac{1}{2}\arctan \left( k \right) \cdot {1^2}} \right]\)

\( = k - \arctan \left( k \right)\)