Problem of the Week #12

■  No GDC  ■

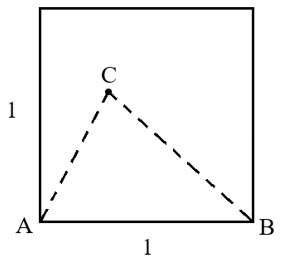
(a)   Consider a unit square (each side is one unit) such that points A and B are two of the vertices of the square. Point C is a randomly chosen point in the interior of the square. Imagine that the location of point C is determined by throwing a dart that sticks somewhere insider the square. Assuming that all points in the interior of the square have an equal probability of being chosen for point C, find the probability that triangle ABC is obtuse.

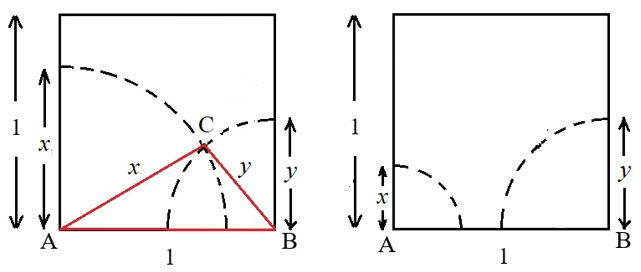
(b)   Again, consider a unit square where A and B are two of the vertices of the square. However, in this case two numbers, \(x\) and \(y\) such that \(0 < x < 1\) and \(0 < y < 1\), are randomly chosen. Imagine that \(x\) is the radius of a circle with its centre at A, and \(y\) is the radius of a circle with its centre at B. If the two circles intersect then the point of intersection is C, the third vertex of triangle ABC (left figure below). It is possible that the randomly chosen numbers for \(x\) and \(y\) are such that the two circles do not intersect (right figure below) resulting in no triangle. So, if \(x\) and \(y\) are random numbers independently chosen from the real numbers between 0 and 1, then find the probability that the three numbers \(x\), \(y\) and 1 are the sides of a triangle ABC, where \({\textrm{AB}} = 1\), such that triangle ABC is obtuse.