 Using a similar process of rearranging and substitution to the suvat equations of linear motion, we can derive equations for rotational motion.
Using a similar process of rearranging and substitution to the suvat equations of linear motion, we can derive equations for rotational motion.
Key Concepts
| Translational | Rotational |
|---|---|
| \(v=u+at\) | \(\omega_f=\omega_i+\alpha t\) |
| \(s={(u+v)\over 2} t\) | \(\theta = {(\omega_i+\omega_f)\over 2} t\) |
| \(s=ut+{1\over 2}at^2\) | \(\theta=\omega_i t+{1\over 2}\alpha t^2\) |
| \(v^2=u^2+2as\) | \({\omega_f}^2={\omega_i}^2+2\alpha \theta\) |
- \(\theta\) is angular displacement (rad)
- \(\omega_i\) is initial angular velocity (rads-1)
- \(\omega_f\) is final angular velocity (rads-1)
- \(\alpha\) is angular acceleration (rads-2)
- \(t\) is the time taken (s)
These equations apply if angular acceleration is constant.
Just as is the case with Newton's second law for forces and motion, an object experiences angular acceleration if it is not in rotational equilibrium.
By substition into Newton's second law, \(F=ma\):
\(\Gamma=I\alpha\)
- \(\Gamma\) is resultant torque (Nm)
- \(I\) is moment of inertia (kgm2)
- \(\alpha\) is angular acceleration (rads-2)
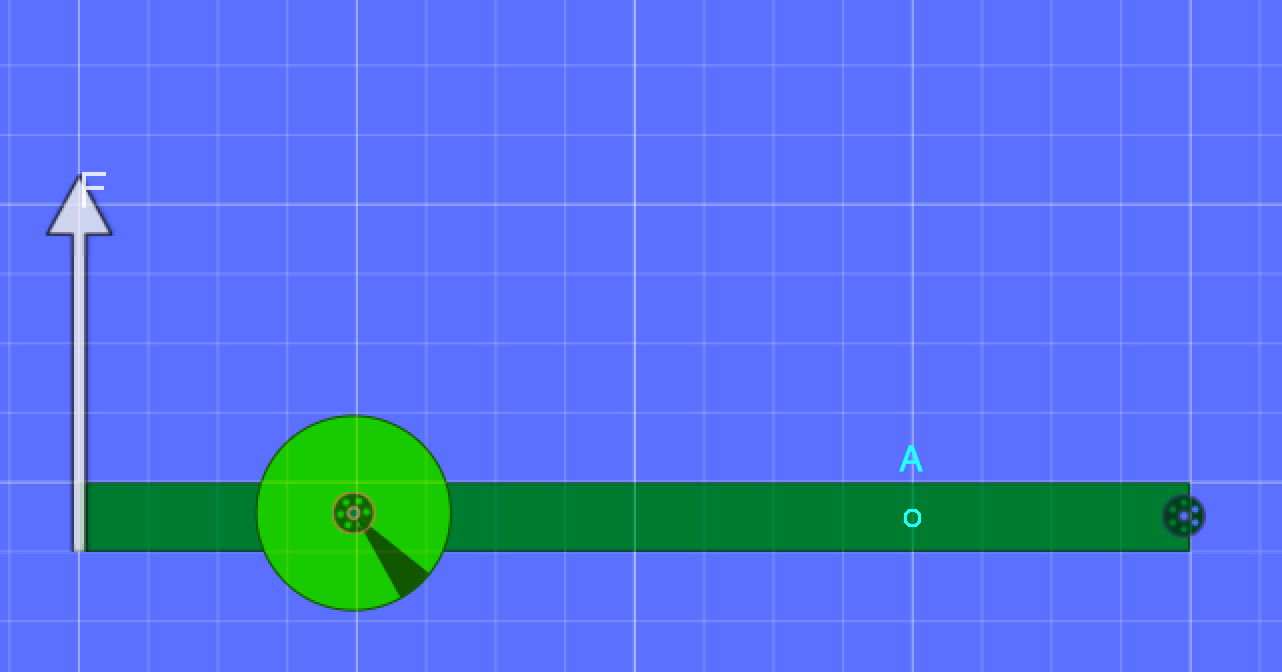
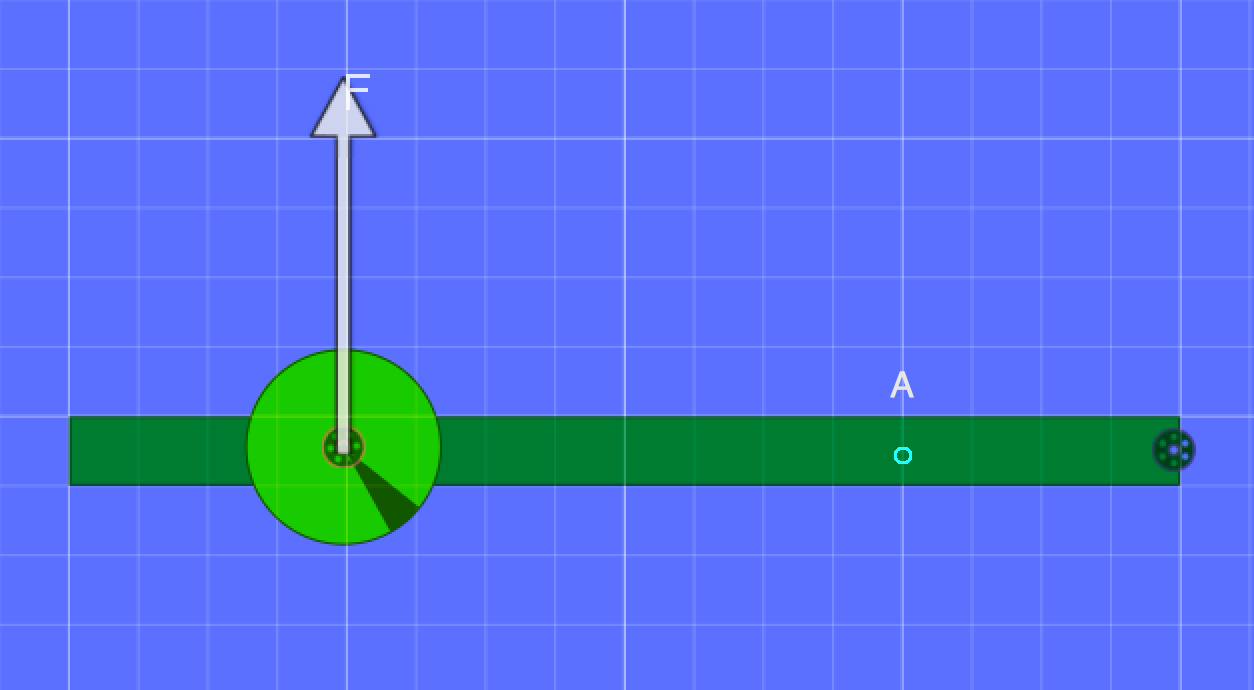
It is important to consider how you might increase angular acceleration. In simple terms, \(\alpha = {\Gamma \over I}\), so angular acceleration increases with torque and decreases with moment of inertia.
A closer examination of the situation below reveals that \(\alpha={Mgr\over Mr^2}={g\over r}\), so only the perpendicular distance has an effect.
.png)
A graph of torque vs time would be proportional in shape to the equivalent angular acceleration graph.
How much of Rotational dynamics have you understood?


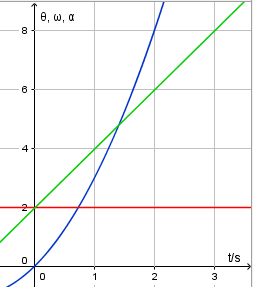 We can also display these quantities on rotational motion graphs.
We can also display these quantities on rotational motion graphs.
 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn