 The rotational equivalent of linear momentum is angular momentum. It is defined as the product of moment of inertia and angular velocity.
The rotational equivalent of linear momentum is angular momentum. It is defined as the product of moment of inertia and angular velocity.
Key Concepts
Angular momentum is the product of moment of intertia and angular velocity:
\(L=I\omega\)
- \(L\) is angular momentum (kgm2s-1)
- \(I\) is moment of inertia (kgm2)
- \(\omega\) is angular velocity (rads-1)
Angular momentum is a conserved quantity: total angular momentum remains constant.
Ice skaters make good use of this effect when spinning.

With limbs spread out, the moment of inertia is high as more mass is at a distance from the pivot. This results in a low angular velocity.

With the limbs closer to the body, the moment of inertia decreases. Since angular momentum is conserved, this increases the angular velocity:
\(I_1\omega_1=I_2\omega_2\)
Rotational kinetic energy is calculated as follows:
\({E_\textrm{K}}_\textrm{rot}={1\over 2}I\omega ^2\)
- \({E_\textrm{K}}_\textrm{rot}\) is rotational kinetic energy (J)
- \(I\) is moment of inertia (kgm2)
- \(\omega\) is angular velocity (rads-1)
Energy is another conserved quantity, with energy changed equal to work done:
\(\Delta {E_\textrm{K}}_\textrm{rot}=\Delta W\)
 Reconsidering our roundabout example, a child would need to do work to move from position A to position B:
Reconsidering our roundabout example, a child would need to do work to move from position A to position B:
- The moment of inertia decreases as the child moves from A to B due to the reduction in radius.
- As a result of conservation of angular momentum, the angular velocity increases by the same proportion.
- Since rotational kinetic energy is proportional to the square of the angular velocity, this effect dominates, resulting in an increase in the rotational kinetic energy.
- The child must do work equal to this change in energy.
How much of Angular momentum and rotational kinetic energy have you understood?


 Conservation of angular momentum also explains why the addition of a child to a spinning roundabout results in a reduction in angular velocity:
Conservation of angular momentum also explains why the addition of a child to a spinning roundabout results in a reduction in angular velocity: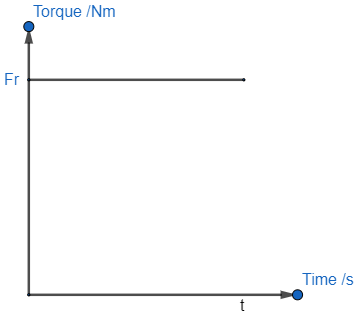 Although not articulated, in the
Although not articulated, in the  If given the same push, a cylinder of equal mass to a hoop would roll more quickly. This is because:
If given the same push, a cylinder of equal mass to a hoop would roll more quickly. This is because:
 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn