 We now understand the diffraction effect of a single slit on light passing through. But what about two slits?
We now understand the diffraction effect of a single slit on light passing through. But what about two slits?
When light passes through two or more slits, it interferes. A pattern can be observed if the waves are coherent. The effect continues with multiple slits or a diffraction grating.
Key Concepts
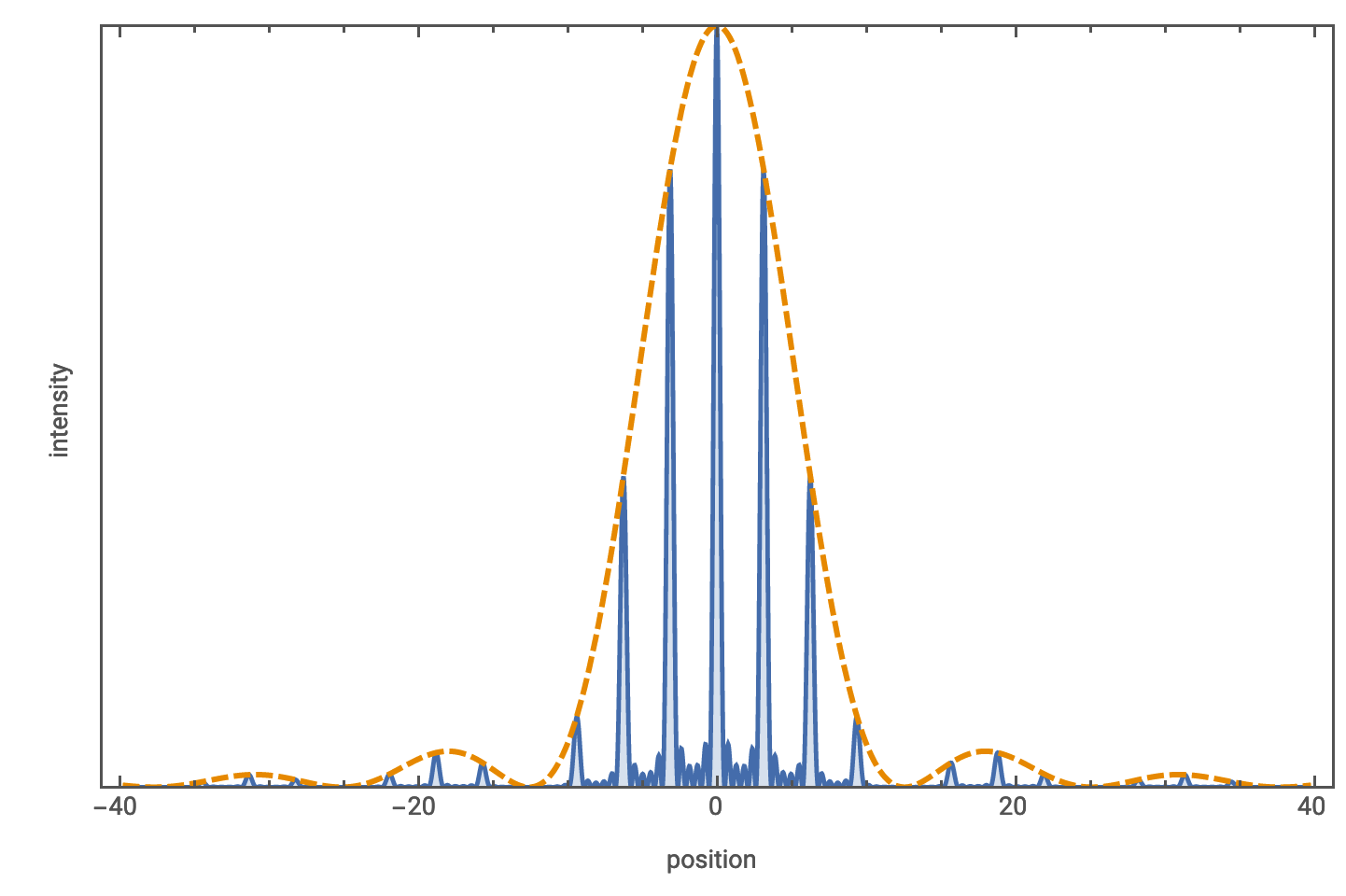
When light shines through multiple slits, an interference pattern forms similar to that through a double slit.
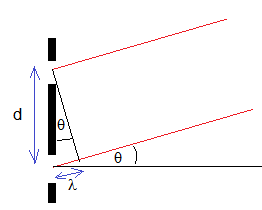
\(n\lambda = d \sin \theta\)
- \(n\) is the number (order) of the maximum, where the central maximum is order 0
- \(\lambda\) is the wavelength of the light (m)
- \(d\) is the distance separating the slits (m)
- \(\theta\) is the angle subtended by the maximum and the centre

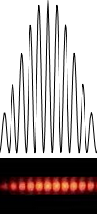
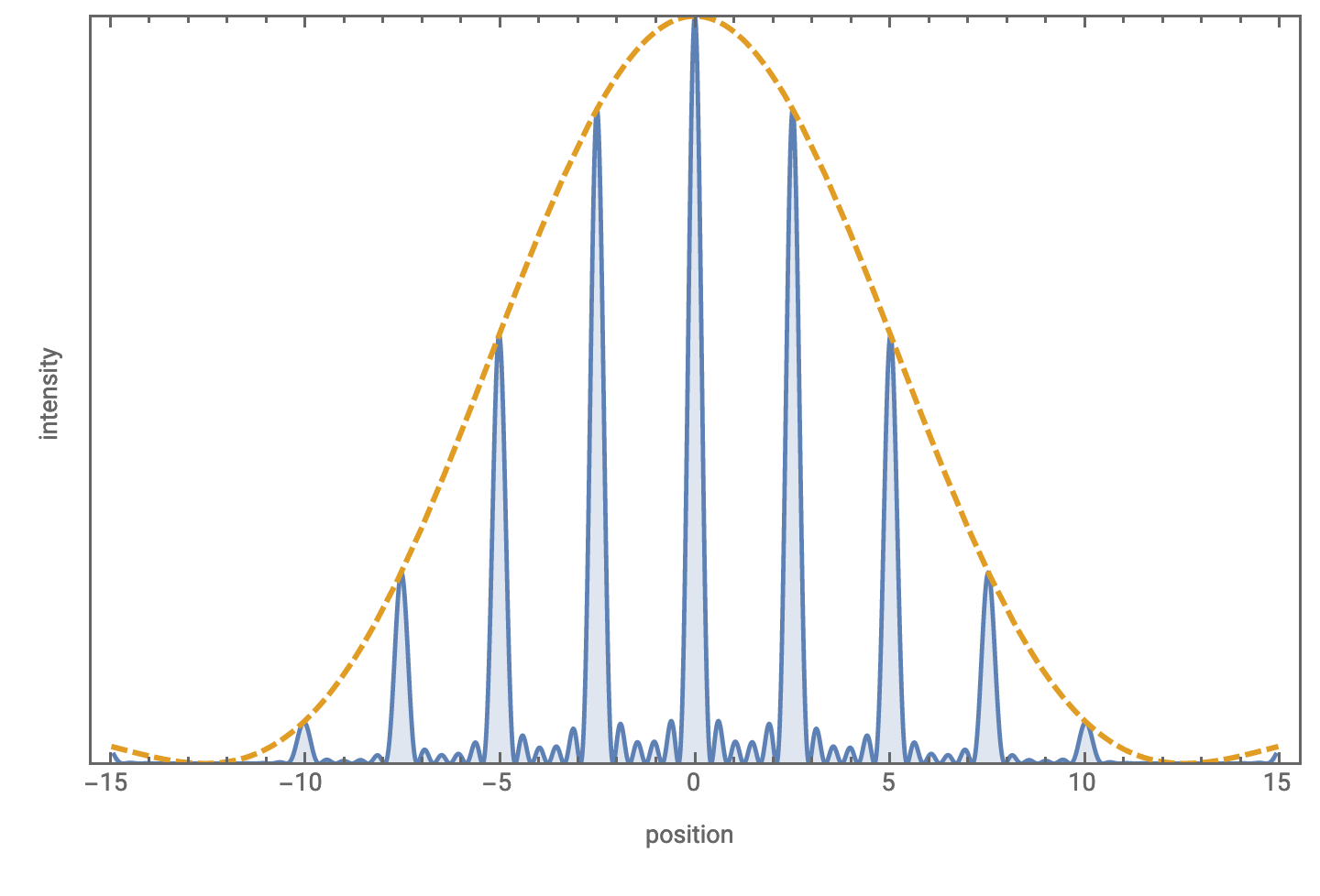
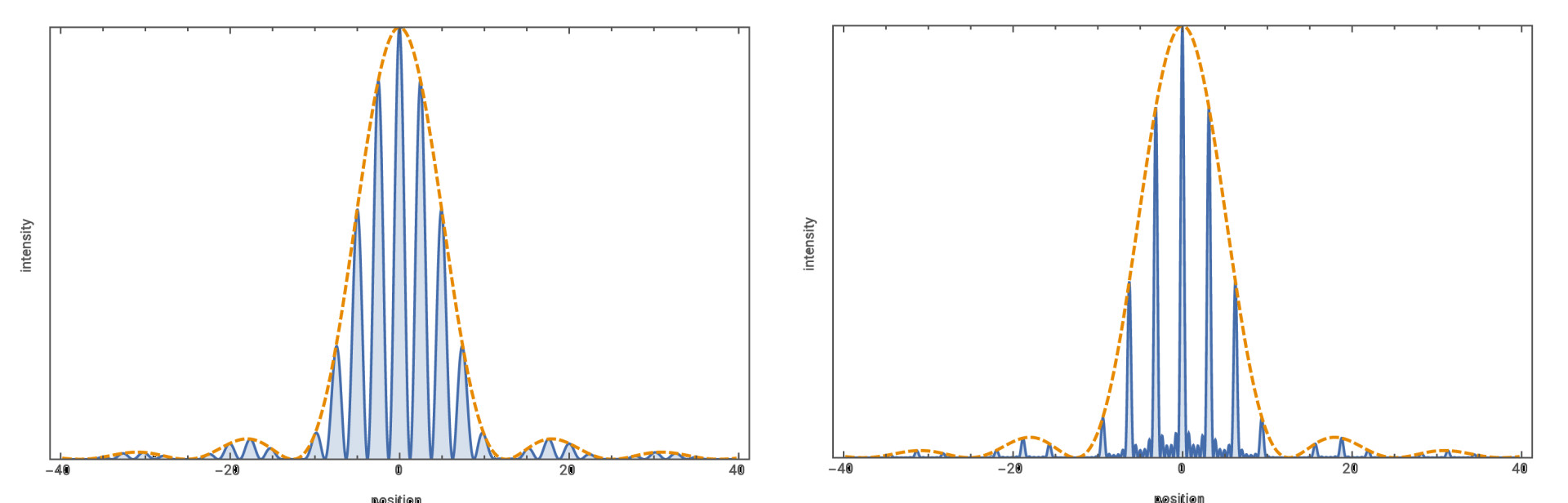
Subsidiary maxima form in between the overall interference maxima.The number of subsidiary maxima produced is equal to the number of slits minus 2.
The ratio of \(\text{slit width}\over \text{separation}\) can be obtained using a combination of the single slit diffraction equation and the multiple slit interference equation. At the first diffraction minimum:
\(\theta = {\lambda\over b}={n\lambda\over d}\Rightarrow {b\over d}={1\over n}\)
Interference patterns emerge from a variety of types of coherent sources such as electromagnetic waves and sound.
Interference can be modelled using a simulation.
How much of Multiple slit interference have you understood?







 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn