 In the Standard Level waves section we established the definition of simple harmonic oscillations: the acceleration of an oscillating body is proportional to displacement but in the opposite direction.
In the Standard Level waves section we established the definition of simple harmonic oscillations: the acceleration of an oscillating body is proportional to displacement but in the opposite direction.
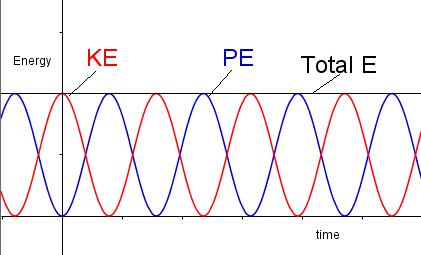
The AHL Waves requirements are more quantitative - displacement, velocity, acceleration, time period, kinetic energy and potential energy must now be calculated at any time.
We recommend that you revise Oscillations before studying this page.
Key Concepts
Simple harmonic motion is defined as motion where the acceleration is directly proportional to the displacement from a fixed point and always acts towards that point.

This definition can be represented by an equation:
\(a = -ω^2x\)
- \(a\) is acceleration (ms-2)
- \(\omega\) is angular frequency: \(\omega=2\pi f={2\pi\over T}\) (Hz)
- \(x\) is displacement (m)
NB: \(f={1\over T}\)
If we assume that the clock starts when the object is released from maximum displacement (the amplitude):
\(x=x_0\cos{\omega t} \Rightarrow v=-\omega x_0\sin \omega t \)
- \(x_0\) is amplitude (m)
- \(t\) is time (s)
- \(v\) is velocity (ms-1)
This velocity is derived by differentiating the displacement equation. Velocity can be found at any time by finding the gradient of displacement. Here the combination is shown (but the maxima of the three would not, in reality, be the same).

\(\)Alternatively, time might 'commence' when the object passes through equililbrium:
\(x=x_0\sin{\omega t} \Rightarrow v=\omega x_0\cos \omega t\)
Also check out: Equations for SHM
A mass oscillating on a spring is an example of simple harmonic motion.

\(T=2\pi \sqrt{m\over k}\)
- \(T\) is time period (s)
- \(m\) is mass (kg)
- \(k\) is spring constant (N m-1)
Also check out: Mass on a spring
How much of Simple harmonic motion have you understood?


.png)
 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn