 This page is aimed to help you with all the basics of probability. You will learn how to list outcomes, how to use Venn diagrams and probability trees. You will also find out about mutually exclusive events and independent events and get plenty of practice in the kind of probability questions that come up in the examinations.
This page is aimed to help you with all the basics of probability. You will learn how to list outcomes, how to use Venn diagrams and probability trees. You will also find out about mutually exclusive events and independent events and get plenty of practice in the kind of probability questions that come up in the examinations.
On this page, you should learn to
- the probability of an event
- complementary events
- expected number of occurrences
- sample spaces
- Venn diagrams
- tree diagrams
- combined events: OR, AND
- mutually exclusive events
- independent events
Here is a quiz that gets you to practise set notation and Venn diagrams
START QUIZ!
Venn Diagrams 1/1
Describe the shaded region below using set notation

This is the intersection of A and B
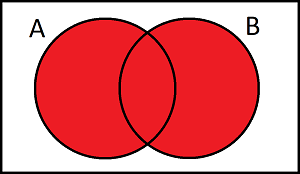
Which of the following Venn diagrams represents \(A\cup B\)
Select all the correct answers
A
| B
|
C
| D
|
\(A\cup B\) is the union of A and B. We shade what is in A and B.
Describe the shaded region below using set notation

The answer is \(A'\cap B\)
- Imagine shading A' and B
- Which region is shaded both times
Describe the shaded region below using set notation

The answer is \(A\cup B'\)
- Imagine shading A and B'
- What region is shaded altogether.
Describe the shaded region below using set notation
Select all the correct answers
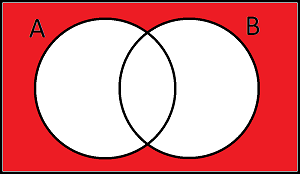
There are two correct answers that describe the same region.
For \((A\cup B)'\) , shade what is outside \(A\cup B\)
For \(A'\cap B'\) , imagine shading A' and B'. The region is what has been shaded twice.
Describe the shaded region below using set notation
Select all the correct answers

There are two correct answers that describe the same region
For \((A\cap B)'\) , shade what is outside \(A\cap B\)
For \(A'\cup B'\), shade A' and B'
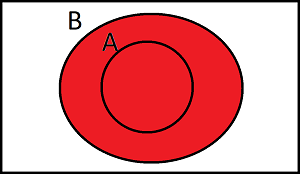
A is a subset of B. Describe the shaded region below using set notation
Select all the correct answers
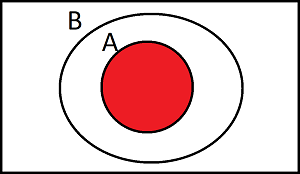
Since A is a subset of B, then \(A\cap B\) also represents this region
A is a subset of B. Describe the shaded region below using set notation
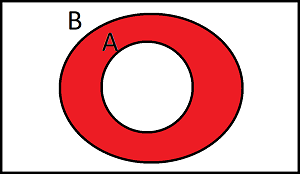
This region is what is in B and not in A
Here is a quiz about mutually exclusive and independent events
START QUIZ!
Mutually Exclusive and Independent Events 1/1
For the two events A and B, \(P(A \cap B)\) = 0
Select all the answers that are true
\(P(A \cap B)\) = 0 means that the two events are mutually exclusive
This means that \(P(A \cup B) =P(A) + P(B) - P(A\cap B) \\ P(A \cup B) =P(A) + P(B) - 0\)
For the two events A and B, \(P(A \cap B) = P(A) \times P(B)\)
Select all the answers that are true
If \(P(A \cap B) = P(A) \times P(B)\), then A and B are independent
Since the probability of A happening is not affected by B, then P(A|B) = P(A)
For the events A and B below, select all the answers that are true
The two events are mutually exclusive and \(P(A \cap B)\)= 0
This means that \(P(A \cup B) =P(A) + P(B) - P(A\cap B) \\ P(A \cup B) =P(A) + P(B) - 0\)
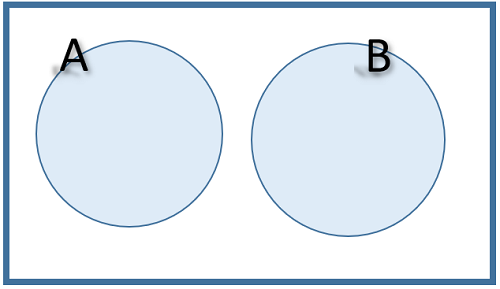
The two events A and B are mutually exclusive. Find the value of x

x =
The two events are mutually exclusive and therefore \(P(A \cap B)\) = 0
The Venn diagram could be drawn with no intersection!
A and B are independent events.
P(A) = 0.3 , P(B') = 0.6.
Work out \(P(A \cap B)\)
\(P(A \cap B)\) =
P(B) = 1 - 0.6 = 0.4
\(P(A \cap B) = P(A) \times P(B)\) = 0.3 x 0.4 = 0.12
A and B are independent events.
P(A) = 0.6 , \(P(A \cap B)\) = 0.54
Work out P(B)
P(B) =
\(P(A \cap B) = P(A) \times P(B)\)
P(B) = 0.54 \(\div \) 0.6 = 0.9
A and B are independent events.
P(A') = 0.6 , P(B) = 0.6
Work out \(P(A \cup B) \)
\(P(A \cup B) \) =
P(A) = 0.4
\(P(A \cap B) = P(A) \times P(B)\) = 0.4x0.6 = 0.24
\(P(A \cup B) =P(A) + P(B) - P(A\cap B) \)
\(P(A \cup B) \) = 0.4 + 0.6 - 0.24 = 0.76
A and B are mutually exclusive events
P(A')= 0.6 , P(B') = 0.65
Work out \(P(A\cup B)\)
\(P(A\cup B)\) =
P(A) = 0.4
P(B) = 0.35
\(P(A\cup B)\) = 0.4 + 0.35
Note that A' and B' are not mutually exclusive
P(A')= 0.5 and P(B') = 0.4
Work out \(P(A' \cap B')\)
\(P(A' \cap B')\) =
P(A) = 0.5 , P(B) = 0.6
\(P(A\cap B)\) = 0.5x0.6 = 0.3
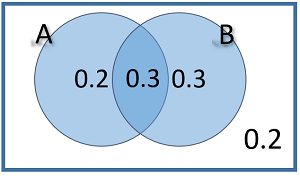
A and B are independent events
P(A) = 0.3 and P(B) = 0.6
Find P(A'|B)
P(A'|B) =
If A and B are independent events
P(A'|B) = P(A')
Here is a quiz about the probability rule \(P(A\cup B)\) = P(A) + P(B) - \(P(A\cap B)\) . You might find Venn diagrams helpful to answer these questions
START QUIZ!
Probability Rules 1/1
Consider two events A and B such that P(A) = 0.5 , P(B) = 0.6 , \(P(A\cap B)\) = 0.25.
Work out \(P(A\cup B)\)
\(P(A\cup B)\) =
\(P(A\cup B)\) = P(A) + P(B) - \(P(A\cap B)\)
= 0.5 + 0.6 - 0.25 = 0.85
Consider two events A and B such that P(B) = 0.38 , \(P(A\cup B)\) = 0.89 , \(P(A\cap B)\) = 0.27.
Work out P(A)
P(A) =
\(P(A\cup B)\) = P(A) + P(B) - \(P(A\cap B)\)
0.89 = P(A) + 0.38 - 0.27
P(A) = 0.78
Consider two events A and B such that P(A) = 0.7 , P(B) = 0.2
Work out \(P(A\cup B)\) if A and B are independent events
\(P(A\cup B)\) =
\(P(A\cap B)\) = P(A)xP(B) = 0.7x0.2 = 0.14
\(P(A\cup B)\) = P(A) + P(B) - \(P(A\cap B)\)
\(P(A\cup B)\) = 0.7 + 0.2 - 0.14 = 0.76
Consider two events A and B such that P(A) = 0.65 , P(B) = 0.31 , \(P(A\cap B)\) = 0.22
Work out \(P(A'\cap B)\)
\(P(A'\cap B)\) =
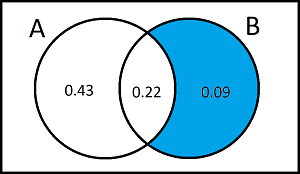
Consider two events A and B such that P(B) = 0.55 , \(P(A\cap B)\) = 0.22.
Work out \(P(A\cap B')\) if A and B are independent
\(P(A\cap B')\) =
\(P(A\cap B)\) = P(A)xP(B)
0.22 = P(A)x0.55
P(A) = 0.4
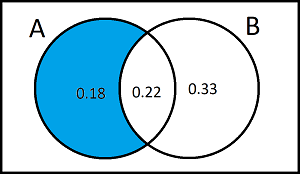
Consider two events A and B such that P(A) = 0.7 , P(B) = 0.6
Work out \(P(A'\cap B')\) if A and B are independent events
\(P(A'\cap B')\) =
\(P(A\cap B)\) = 0.7x0.6 = 0.42
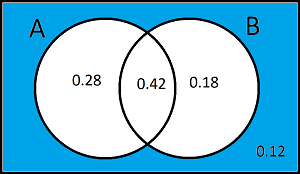
Consider two events A and B such that \(P(A\cup B)'\) = 0.22 , \(P(A'\cap B)\) = 0.34
Work out P(A)
P(A) =
P(A) = 1 - 0.34 - 0.22

Consider two events A and B such that P(A) = 0.5 , P(B) = 0.7.
Work out \(P(A'\cup B)\) if A and B are independent events
\(P(A\cap B)\) =
\(P(A\cap B)\) = 0.5 x 0.7 = 0.35

Consider two events A and B such that P(A) = 0.3 , P(B) = 0.5.
Find \(P(A\cup B)\) if \(P(A\cup B) = 3P(A\cap B)\)
\(P(A\cup B)\) =
\(P(A\cup B)\) = P(A) + P(B) - \(P(A\cap B)\)
\( 3P(A\cap B)\) = 0.3 + 0.5 - \( P(A\cap B)\)
Treat this as an equation and solve. You can even substitute \(P(A\cap B)\) = x
3x = 0.8 - x
4x = 0.8
x = 0.2
\(P(A\cap B)\) = 0.2
\(P(A\cup B)\) = 3 x 0.2 = 0.6
Consider two events A and B such that \(P(A\cup B)\) = 0.8 , P(A) = 0.6
Given that A and B are independent, find P(B)
P(B) =
\(P(A\cap B)\) = 0.6P(B)
\(P(A\cup B)\) = P(A) + P(B) - \(P(A\cap B)\)
0.8 = 0.6 + P(B) - 0.6P(B)
Treat this as an equation and solve. You can even substitute P(B) = x
0.8 = 0.6 + x - 0.6x
0.2 = 0.4x
x = 0.5
P(B) = 0.5
The final quiz on this page is about independent events. You might find tree diagrams helpful to answer these questions
START QUIZ!
Independent Events 1/1
A bag contains 3 red balls and 2 white balls. A ball is selected at random. Without replacing the first, a second ball is selected. Find the probability that 2 red balls are selected.
probability =
The probability that the first ball is red is \(\frac {3}{5}\)
The probability that the second ball is red is \(\frac {2}{4}\)
Probability of red AND red = \(\frac {3}{5} \times \frac {2}{4} = \frac {6}{20}\)
Three fair coins are flipped. Find the probability that 2 heads are flipped.
Here are all 8 possible outcomes
HHH
HHT
HTH
THH
TTH
THT
HTT
TTT
There are 3 outcomes with 2 heads
A bag contains 3 green balls and 2 other coloured balls. A ball is taken at random then replaced. A second ball is taken. Find the probability that 2 green balls are taken.
probability =
probability = \(\frac {3}{5} \times \frac {3}{5}=\frac {9}{25}\)
A drawer contains 4 black socks and 6 stripey socks. Two socks are drawn at random. The probability that 2 black socks are taken is \(\frac {a}{15}\).
Find a
a =
\(\frac {4}{10}\times \frac {3}{9}=\frac {12}{90}=\frac {2}{15}\)
A bag contains 7 black and 3 white balls. Two balls are taken at random.
The probability that both balls are the same colour is \(\frac {a}{15}\)
Work out a
a =
probability of BB OR WW = \(\frac {7}{10}\times \frac {6}{9}+\frac {3}{10}\times \frac {2}{9}\) = \(\frac {42}{90}+\frac {6}{90}=\frac {48}{90}=\frac {8}{15}\)
A drawer contains 2 black, 4 grey and 6 white socks. Two socks are drawn at random. Find the probability that they are the same colour.
probability (BB OR GG OR WW) = \(\frac {2}{12}\times\frac {1}{11}+\frac {4}{12}\times\frac {3}{11}+\frac {6}{12}\times\frac {5}{11}\)
= \(\frac {2}{132}+\frac {12}{132}+\frac {30}{132}=\frac {44}{132}\)
The probability that a sportsperson is left-handed is 0.12.
The probability that a sportsperson is left-handed and left-footed is 0.102.
The probability that a sportsperson is right-handed and right-footed is 0.792.
Work out a , b , c and d in the probability tree below
a =
b =
c =
d =
0.12 x a = 0.102
a = 0.85
b = 0.15
0.88 x d = 0.792
d = 0.9
c = 0.1
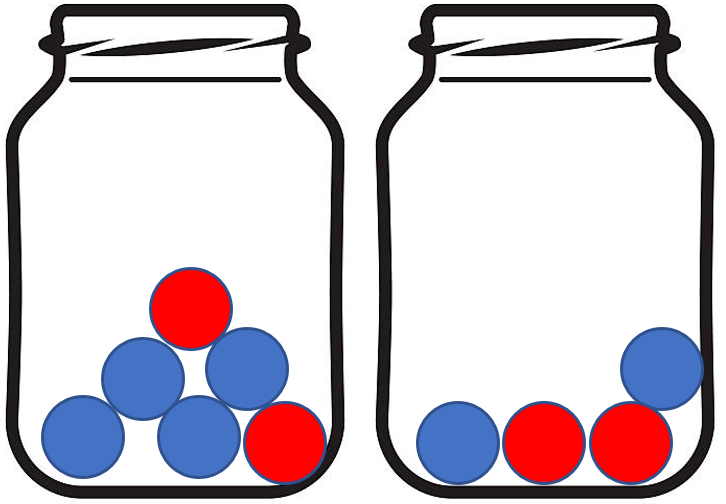
Jar A contains 4 blue marbles and 2 red marbles.
Jar B contains 2 blue marbles and 2 red marbles.
A marble is taken at random from jar A and placed in jar B. Next, a marble is taken from jar B and placed in jar A.
After this, the probability that there are still 4 blue marbles in jar A is \(\frac{a}{30}\).
Work out a
a =
There are two possibilities so that there are 4 marbles in jar A
1) A blue is taken from jar A and put into jar B (there will be 3 blue and 2 red in jar B)
2) A red is taken from jar A and put into jar B (there will be 2 blue and 3 red in jar B)
Probability (B1, B2 OR R1,R2) = \(\frac{4}{6}\times \frac{3}{5}+\frac{2}{6}\times \frac{3}{5}\) = \(\frac{18}{30}\)
Maria drives to work.
The probability that she is late when it rains is 0.6
The probability that she is late when it does not rain is 0.1
In November, the probability that it rains on the drive to work is 0.4
a) On a particular day in November, find the probability that she is late for work
b) She will be disciplined at work if she is late (at least) twice in 3 consecutive days. It is a Monday morning in November, find the probability that she will disciplined on Wednesday.
a) probability that she is late for work =
b) probability that she will disciplined =
a) probability (rain AND late OR not rain AND late) = 0.4 x 0.6 + 0.6 x 0.1 = 0.3
b) Let L = late , \(\overline{L}\) = not late
There are 4 possible outcomes to be disciplined
\(\overline{L}LL\\ L\overline{L}L\\ LL\overline{L}\\ LLL\)
Note that she will also be disciplined if she is late on all three days
\(3 \times0.3^2\times0.7 \ + \ 0.3^3\) = 0.216
In order to revise for her IB examinations, a student sits 3 practice papers.
The probability that she achieves a grade 7 on the first paper is 0.2
Whenever she gains a grade 7 in a paper, she becomes more confident and the probability of getting a grade 7 on the next paper increases by 0.1
However, whenever she does not get a grade 7 in a paper, the probability of getting a grade 7 on the next paper decreases by 0.05
Complete the following probability tree
Find the probability that she gets exactly two grade 7s on the practice papers.
probability =
Here is the completed probability tree showing the three possible ways of getting exactly 2 grade 7 results

probability = 0.036 + 0.035 + 0.03 = 0.101
text



Two events A and B are such that P(A) = 0.35 and P(B) = 0.6 and \(P(A\cup B)\) = 0.74
a) Find \(P(A\cap B)\)
b) Determine whether A and B are independent
c) Find \(P(A'\cap B)\)
Hint
b) If A and B are independent \(P(A\cap B)=P(A)\times P(B)\)
Full Solution
Print from here



Katniss is practising archery. She fires three arrows at a target. The probability that she hits the target with her first arrow is 0.7. Whenever she hits the target, her confidence increases so that the probability that she hits the target on her next attempt increases by 0.1. Whenever she misses the target, the probability reduces by 0.1.
 a) Complete the probability tree for Katniss’s three attempts.
a) Complete the probability tree for Katniss’s three attempts.
b) Calculate the probability that she hits the target with two attempts.
c) Find the probability the she hits the target on at least one attempt.
Hint
a) Fill out the probability tree carefully, the probability of hits and misses changes each time
Full Solution
Print from here


Events A and B are such that P(A) = 0.4 and \(P(A\cup B)\) = 0.7
Find P(B) if A and B are independent
Hint
If A and B are independent, then \(P(A\cap B) =P(A)\times P(B)\)
Write an equation and consider writing P(B) = x
Full Solution
Print from here


Alphonse and Bettina are playing a game. A bag contains 2 yellow beads and 3 red beads. They take it in turns to pick a bead from the bag at random. Alphonse goes first. If Alphonse picks a yellow bead, he wins and the game stops. If he picks a red bead, he replaces the bead and it is Bettina’s turn. If Bettina picks a red bead, she wins and the game stops. If she picks a yellow bead, she replaces the bead and it is Alphonse’s turn again.

a) Find the probability that Alphonse wins on his first turn.
b) Show that the probability that Alphonse wins on his second turn is \(\frac{12}{125}\)
c) The game continues until one of the player wins. What is the probability that Alphonse wins the game?
Hint
c) The probability that Alphonse wins is the sum of an infinite geometric series \({ S }_{ \infty }=\frac { { U }_{ 1 } }{ 1-r } \)
Full Solution
Print from here



A box contains 25 tickets. x tickets are gold, the rest are silver. Two tickets are selected at random.
a) Show that the probability of selecting two gold tickets is \(\frac{x^2-x}{600}\)
b) Find the probability of selecting two tickets of the same colour.
c) The probability of selecting two tickets of the same colour is twice the probability of selecting two tickets of a different colour. Find how many gold tickets there are.
Hint
b) Find probability of GG or SS
c) If the probability of selecting two tickets of the same colour is twice the probability of selecting two tickets of a different colour, then the probability of selecting two tickets of the same colour = \(\frac{2}{3}\)
Full Solution
Print from here
How much of Probability Calculations have you understood?
Feedback
Which of the following best describes your feedback?



 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn