 On this page we will explore the concept of discrete random variables and their probability distributions. We will look at how we can display probability distributions in tables or as functions. The questions are not so complicated (it is just a way of formalising the language of probability), for example, it is important not to forget that probabilities still add up to 1!
On this page we will explore the concept of discrete random variables and their probability distributions. We will look at how we can display probability distributions in tables or as functions. The questions are not so complicated (it is just a way of formalising the language of probability), for example, it is important not to forget that probabilities still add up to 1!
On this page, you should learn about
- discrete random variables
- probability distributions
- mean (expected value)
- variance (HL only)
Print from here
MY PROGRESS
How much of Discrete Random Variables have you understood?






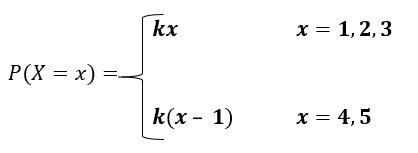










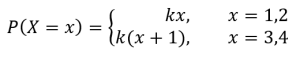



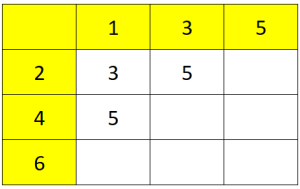


 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn