5.6.2 Calculus for Kinematics

Displacement, velocity and acceleration are related by calculus
In terms of differentiation and derivatives
- velocity is the rate of change of displacement
  - $v = \frac{d s}{d t}$ or $v (t) = s' (t)$
- acceleration is the rate of change of velocity
  - $a = \frac{d v}{d t}$ or $a (t) = v' (t)$
- so acceleration is also the second derivative of displacement
  - $a = \frac{d^{2} s}{d t^{2}}$ or $a (t) = s'' (t)$
If a graph is not given you can use your GDC to draw one
- you can then use your GDC’s graphing features to find gradients
  - velocity is the gradient on a displacement (-time) graph
  - acceleration is the gradient on a velocity (-time) graph

The displacement, $s m$ , of a particle at $t$ seconds, is modelled by $s (t) = 2 t^{3} - 27 t^{2} + 84 t$

5-6-2-ib-sl-aa-only-diffk-we-soltn

Since velocity is the derivative of displacement ( $v = \frac{d s}{d t}$ ) it follows that

$s = \int v d t$

$v = \int a d t$

A boundary or initial condition would need to be known
- phrases involving the word “initial”, or “initially” are referring to time being zero, i.e. $t = 0$
- you might also be given information about the object at some other time (this is called a boundary condition)
- substituting the values in from the initial or boundary condition would allow the constant of integration to be found

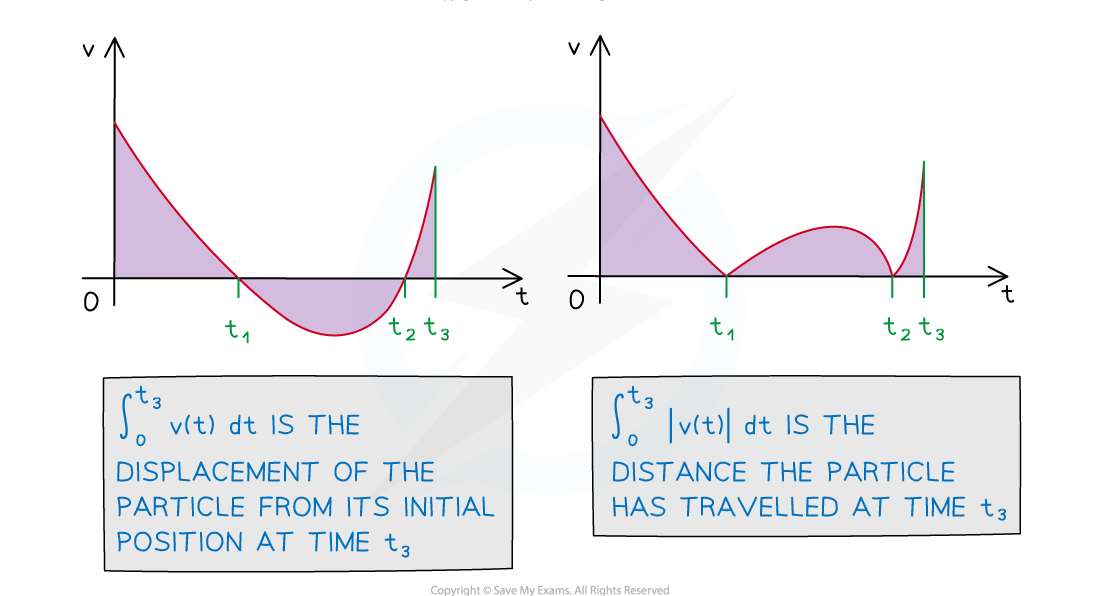
5-6-2-ib-sl-aa-only-kin-mod-graph

Sketching the velocity-time graph can help you visualise the distances travelled using areas between the graph and the horizontal axis

A particle moving in a straight horizontal line has velocity ( $v m s^{- 1}$ ) at time $t$ seconds modelled by $v (t) = 8 t^{3} - 12 t^{2} - 2 t$ .

Given that the initial position of the particle is at the origin, find an expression for its displacement from the origin at time $t$ seconds.
Find the displacement of the particle from the origin in the first five seconds of its motion.
Find the distance travelled by the particle in the first five seconds of its motion.

5-6-2-ib-sl-aa-only-int-kin-we-soltn

DP IB Maths: AA SL

5.6.2 Calculus for Kinematics