Binomial Theorem
What is the Binomial Theorem?
- The binomial theorem (sometimes known as the binomial expansion) gives a method for expanding a two-term expression in a bracket raised to a power
- A binomial expression is in fact any two terms inside the bracket, however in IB the expression will usually be linear
- To expand a bracket with a two-term expression in:
- First choose the most appropriate parts of the expression to assign to a and b
- Then use the formula for the binomial theorem:
-
- where
- See below for more information on
- You may also see
written as
or
- See below for more information on
- where
- You will usually be asked to find the first three or four terms of an expansion
- Look out for whether you should give your answer in ascending or descending powers of x
- For ascending powers start with the constant term, an
- For descending powers start with the term with x in
- You may wish to swap a and b over so that you can follow the general formula given in the formula book
- If you are not writing the full expansion you can either
- show that the sequence continues by putting an ellipsis (…) after your final term
- or show that the terms you have found are an approximation of the full sequence by using the sign for approximately equals to (≈)
How do I find the coefficient of a single term?
- Most of the time you will be asked to find the coefficient of a term, rather than carry out the whole expansion
- Use the formula for the general term
- The question will give you the power of x of the term you are looking for
- Use this to choose which value of r you will need to use in the formula
- This will depend on where the x is in the bracket
- The laws of indices can help you decide which value of r to use:
- For
to find the coefficient of
use
- For
to find the coefficient of
use
- For
look at how the powers will cancel out to decide which value of
to use
- So for
to find the coefficient of
use the term with
and to find the constant term use the term with
- There are a lot of variations of this so it is usually easier to see this by inspection of the exponents
- For
- You may also be given the coefficient of a particular term and asked to find an unknown in the brackets
- Use the laws of indices to choose the correct term and then use the binomial theorem formula to form and solve and equation
Exam Tip
- Binomial expansion questions can get messy, use separate lines to keep your working clear and always put terms in brackets
Worked Example
Find the first three terms, in ascending powers of , in the expansion of
.

The Binomial Coefficient nCr
What is  ?
?
- If we want to find the number of ways to choose r items out of n different objects we can use the formula for
- The formula for r combinations of n items is
- This formula is given in the formula booklet along with the formula for the binomial theorem
- The function
can be written
or
and is often read as ‘n choose r’
- Make sure you can find and use the button on your GDC
- The formula for r combinations of n items is
How does  relate to the binomial theorem?
relate to the binomial theorem?
- The formula
is also known as a binomial coefficient
- For a binomial expansion
the coefficients of each term will be
,
and so on up to
- The coefficient of the
term will be
- The coefficient of the
- The binomial coefficients are symmetrical, so
- This can be seen by considering the formula for
- This can be seen by considering the formula for
Exam Tip
- You will most likely need to use the formula for nCr at some point in your exam
- Practice using it and don't always rely on your GDC
- Make sure you can find it easily in the formula booklet
Worked Example
Without using a calculator, find the coefficient of the term in in the expansion of
.

Pascal's Triangle
What is Pascal’s Triangle?
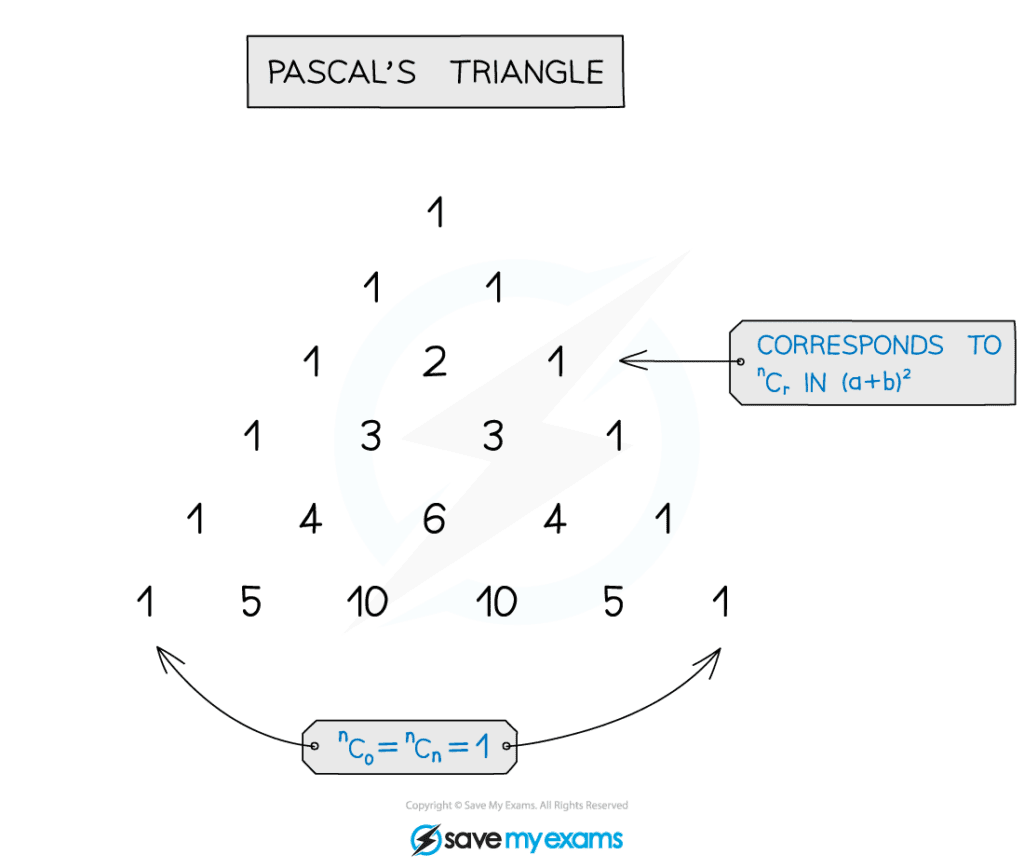
- Pascal’s triangle is a way of arranging the binomial coefficients and neatly shows how they are formed
- Each term is formed by adding the two terms above it
- The first row has just the number 1
- Each row begins and ends with a number 1
- From the third row the terms in between the 1s are the sum of the two terms above it
How does Pascal’s Triangle relate to the binomial theorem?
- Pascal’s triangle is an alternative way of finding the binomial coefficients,
- It can be useful for finding for smaller values of
without a calculator
- However for larger values of
it is slow and prone to arithmetic errors
- It can be useful for finding for smaller values of
- Taking the first row as zero,
, each row corresponds to the
row and the term within that row corresponds to the
term
Exam Tip
- In the non-calculator exam Pascal's triangle can be helpful if you need to get the coefficients of an expansion quickly, provided the value of n is not too big
Worked Example
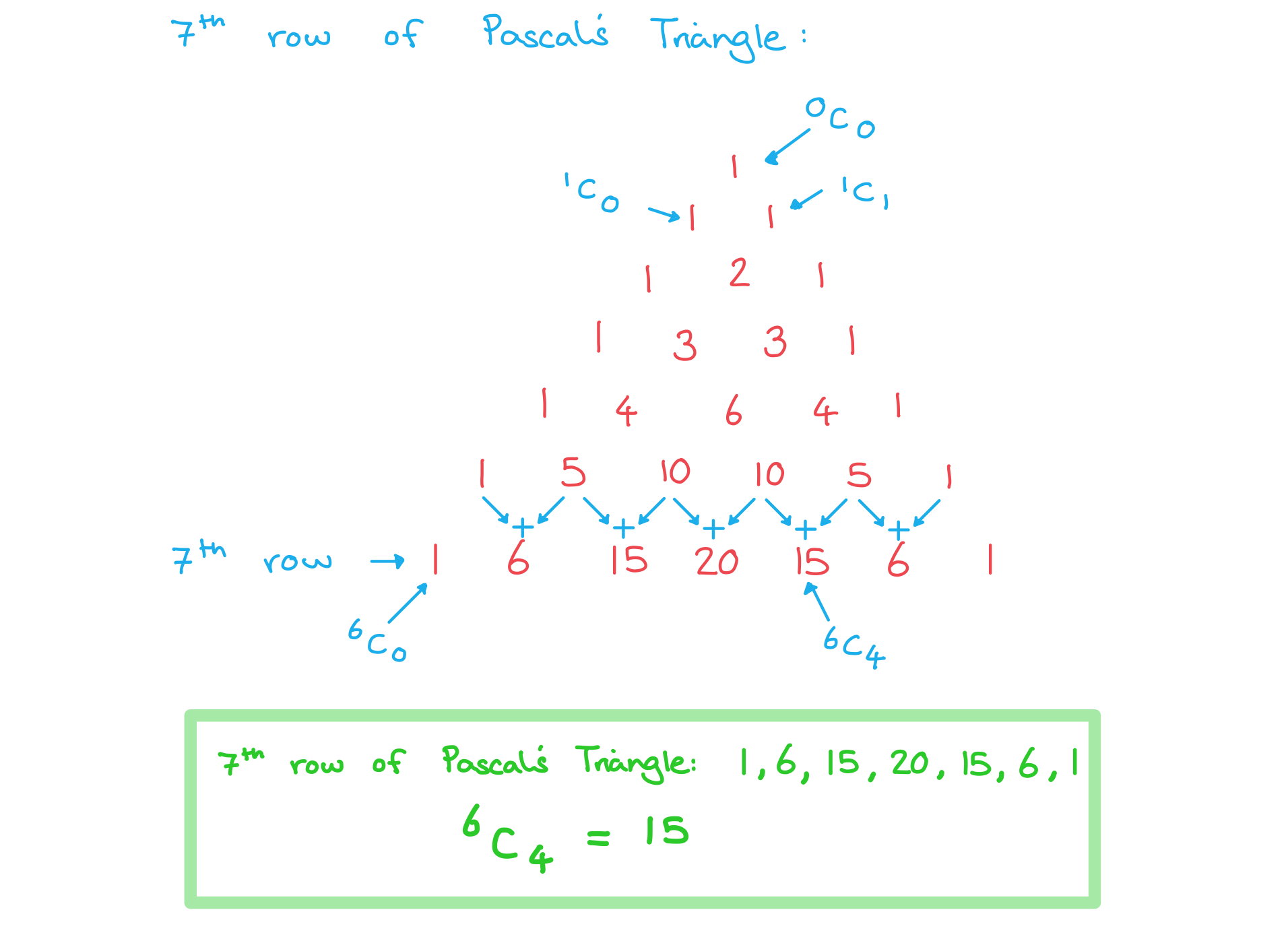
Write out the 7th row of Pascal’s triangle and use it to find the value of .