3.4.1 The Unit Circle

What is the unit circle?

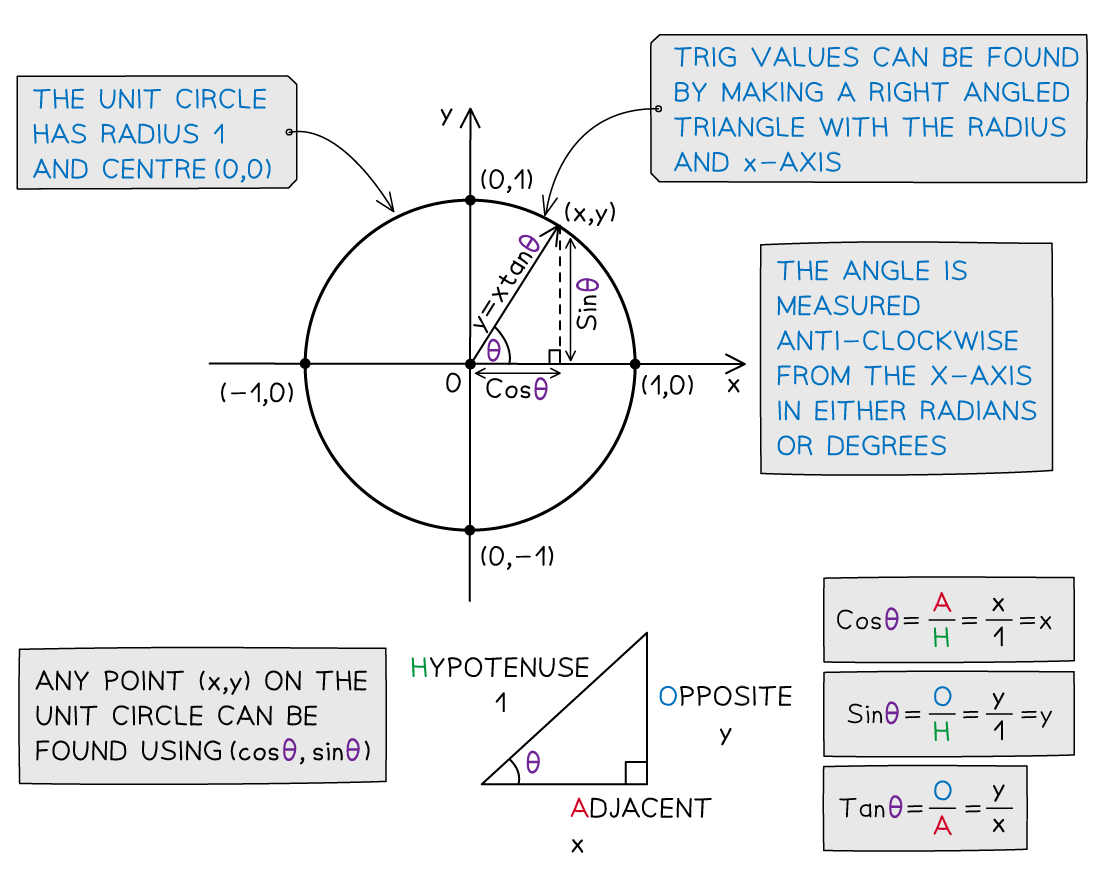
• The unit circle is a circle with radius 1 and centre (0, 0)
• Angles are always measured from the positive x-axis and turn:
  • anticlockwise for positive angles
  • clockwise for negative angles
• It can be used to calculate trig values as a coordinate point (x, y) on the circle
  • Trig values can be found by making a right triangle with the radius as the hypotenuse
  • Where θ is the angle measured anticlockwise from the positive x-axis
  • The x-axis will always be adjacent to the angle, θ
• SOHCAHTOA can be used to find the values of sinθ, cosθ and tanθ easily
• As the radius is 1 unit
  • the x coordinate gives the value of cosθ
  • the y coordinate gives the value of sinθ
• As the origin is one of the end points - dividing the y coordinate by the x coordinate gives the gradient
  • the gradient of the line gives the value of tanθ
• It allows us to calculate sin, cos and tan for angles greater than 90° (rad)

Worked Example

What are the properties of the unit circle?

• The unit circle can be split into four quadrants at every 90° ( rad)
  • The first quadrant is for angles between 0 and 90° 
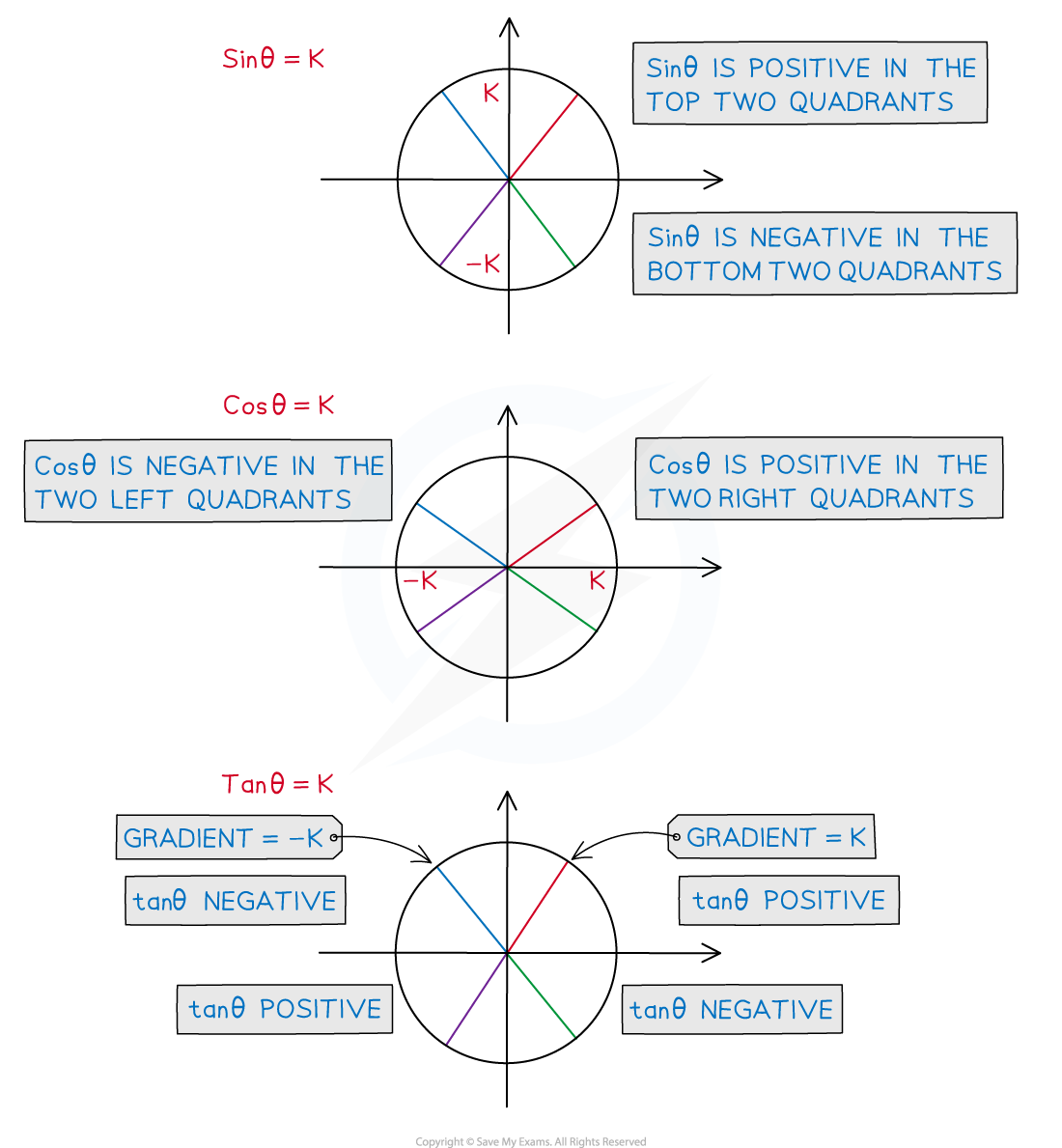
    • All three of Sinθ, Cosθ and Tanθ are positive in this quadrant
  • The second quadrant is for angles between 90° and 180° ( rad and  rad)
    • Sinθ is positive in this quadrant
  • The third quadrant is for angles between 180° and 270° ( rad and )
    • Tanθ is positive in this quadrant
  • The fourth quadrant is for angles between 270° and 360° ( rad and )
    • Cosθ is positive in this quadrant
  • Starting from the fourth quadrant (on the bottom right) and working anti-clockwise the positive trig functions spell out CAST
    • This is why it is often thought of as the CAST diagram
    • You may have your own way of remembering this
    • A popular one starting from the first quadrant is All Students Take Calculus
  • To help picture this better try sketching all three trig graphs on one set of axes and look at which graphs are positive in each 90° section

How is the unit circle used to find secondary solutions?

• Trigonometric functions have more than one input to each output
  • For example sin 30° = sin 150° = 0.5
  • This means that trigonometric equations have more than one solution
  • For example both 30° and 150° satisfy the equation sin x = 0.5
• The unit circle can be used to find all solutions to trigonometric equations in a given interval
  • Your calculator will only give you the first solution to a problem such as x = sin^-1(0.5)
    • This solution is called the primary value
  • However, due to the periodic nature of the trig functions there could be an infinite number of solutions
    • Further solutions are called the secondary values
  • This is why you will be given a domain in which your solutions should be found
    • This could either be in degrees or in radians
    • If you see π or some multiple of π then you must work in radians
• The following steps may help you use the unit circle to find secondary values

STEP 1: Draw the angle into the first quadrant using the x or y coordinate to help you

• If you are working with sin x = k, draw the line from the origin to the circumference of the circle at the point where the y coordinate is k
• If you are working with cos x = k, draw the line from the origin to the circumference of the circle at the point where the x coordinate is k
• If you are working with tan x = k, draw the line from the origin to the circumference of the circle such that the gradient of the line is k
  • This will give you the angle which should be measured from the positive x-axis…
    • … anticlockwise for a positive angle
    • … clockwise for a negative angle

STEP 2: Draw the radius in the other quadrant which has the same...

• ... x-coordinate if solving cos x = k
  • This will be the quadrant which is vertical to the original quadrant
• ... y-coordinate if solving sin x = k
  • This will be the quadrant which is horizontal to the original quadrant
• ... gradient if solving tan x = k
  • This will be the quadrant diagonal to the original quadrant

STEP 3: Work out the size of the second angle, measuring from the positive x-axis

• … anticlockwise for a positive angle
• … clockwise for a negative angle
  • You should look at the given range of values to decide whether you need the negative or positive angle

STEP 4: Add or subtract either 360° or 2π radians to both values until you have all solutions in the required range

Exam Tip

Worked Example