3.4.2 Exact Values

For certain angles the values of sin θ, cos θ and tan θ can be written exactly
- This means using fractions and surds
- You should be familiar with these values and be able to derive the values using geometry
You are expected to know the exact values of sin, cos and tan for angles of 0°, 30°, 45°, 60°, 90°, 180° and their multiples
- In radians this is $0, \frac{π}{6}, \frac{π}{4}, \frac{π}{3}, \frac{π}{2}, π$ and their multiples
The exact values you are expected to know are here:

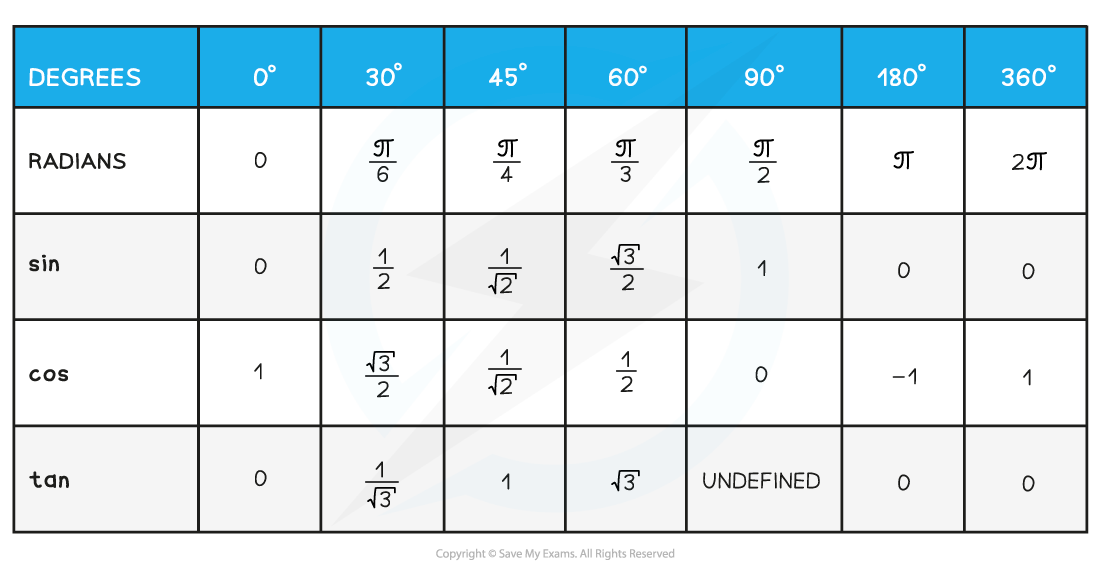
5-4-2-exact-values-notes-diagram-3-1

The exact values for sin and cos can be seen on the unit circle as the y and x coordinates respectively
- If using the coordinates on the unit circle to memorise the exact values, remember that cos comes before sin
The unit circle can also be used to find exact values of other angles using symmetry
If you know the exact value for an angle in the first quadrant you can draw the same angle from the x-axis in any other quadrant to find other angles
Remember that the angles are measured anticlockwise from the positive x-axis
For example if you know that the exact value for is 0.5
- draw the angle 30° from the horizontal in the three other quadrants
- measuring from the positive x-axis you have the angles of 150°, 210° and 330°
  - sin is positive in the second quadrant so sin150° = 0.5
  - sin is negative in the third quadrant so sin210° = - 0.5
  - sin is negative in the fourth quadrant so sin330° = - 0.5
It is also possible to find the negative angles by measuring clockwise from the positive x-axis
- draw the angle 30° from the horizontal in the three other quadrants
- measuring clockwise from the positive x-axis you have the angles of -30°, -150°, -210° and -330°
  - sin is negative in the fourth quadrant so sin(-30°) = - 0.5
  - sin is negative in the third quadrant so sin(-150°) = - 0.5
  - sin is positive in the second quadrant so sin(-210°) = 0.5
  - sin is positive in the fourth quadrant so sin(-330°) = 0.5

ib-aa-sl-3-4-exact-values-diagram-1

There are two special right-triangles that can be used to derive all of the exact values you need to know
Consider a right-triangle with a hypotenuse of 2 units and a shorter side length of 1 unit
- Using Pythagoras’ theorem the third side will be $\sqrt{3}$
- The angles will be $\frac{π}{2}$ radians (90°), $\frac{π}{3}$ radians (60°) and $\frac{π}{6}$ radians (30°)
- Using SOHCAHTOA gives…
  - Sin $\frac{π}{3}$ = $\frac{\sqrt{3}}{2}$ Sin $\frac{π}{6}$ = $\frac{1}{2}$
  - Cos $\frac{π}{3}$ = $\frac{1}{2}$ Cos $\frac{π}{6}$ = $\frac{\sqrt{3}}{2}$
  - Tan $\frac{π}{3}$ = $\sqrt{3}$ Tan $\frac{π}{6}$ = $\frac{1}{\sqrt{3}}$ = $\frac{\sqrt{3}}{3}$
Consider an isosceles triangle with two equal side lengths (the opposite and adjacent) of 1 unit
- Using Pythagoras’ theorem it will have a hypotenuse of $\sqrt{2}$
- The two equal angles will be $\frac{π}{4}$ radians (45°)
- Using SOHCAHTOA gives…
  - Sin $\frac{π}{4} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$
  - Cos $\frac{π}{4} = \frac{1}{\sqrt{2}} = \frac{\sqrt{2}}{2}$
  - Tan $\frac{π}{4}$ = 1

5-4-2-exact-values-notes-diagram-1

You will be expected to be comfortable using exact trig values for certain angles but it can be easy to muddle them up if you just try to remember them from a list, sketch the triangles and trig graphs on your paper so that you can use them as many times as you need to during the exam!
- sketch the triangles for the key angles $45 °$ / $\frac{π}{4}$ , $30 °$ / $\frac{π}{6}$ , $60 °$ / $\frac{π}{3}$
- sketch the trig graphs for the key angles $0 °$ , $90 °$ / $\frac{π}{2}$ , $180 °$ / $π$ , $270 °$ / $\frac{3 π}{2}$ , $360 °$ / $2 π$

Using an equilateral triangle of side length 2 units, derive the exact values for the sine, cosine and tangent of $\frac{π}{6}$ and $\frac{π}{3}$ .

aa-sl-3-4-2-trig-exact-values-we-solution

DP IB Maths: AA SL

3.4.2 Exact Values