IB Questionbank

User interface language: English | Español

Date	May 2022	Marks available	5	Reference code	22M.2.SL.TZ1.4
Level	Standard Level	Paper	Paper 2	Time zone	Time zone 1
Command term	Find	Question number	4	Adapted from	N/A

Question

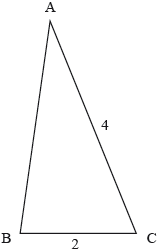
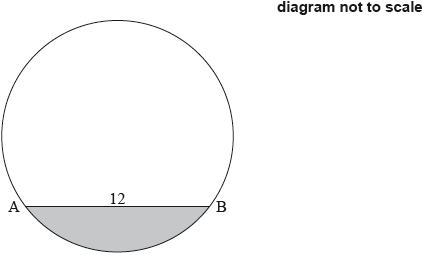
A sector of a circle, centre $O$ and radius $4.5 m$ , is shown in the following diagram.

A square field with side $8 m$ has a goat tied to a post in the centre by a rope such that the goat can reach all parts of the field up to $4.5 m$ from the post.

^{[Source: mynamepong, n.d. Goat [image online] Available at: https://thenounproject.com/term/goat/1761571/}
^{This file is licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported (CC BY-SA 3.0)}
^{https://creativecommons.org/licenses/by-sa/3.0/deed.en [Accessed 22 April 2010] Source adapted.]}

Let $V$ be the volume of grass eaten by the goat, in cubic metres, and $t$ be the length of time, in hours, that the goat has been in the field.

The goat eats grass at the rate of $\frac{d V}{d t} = 0.3 t e^{- t}$ .

Find the angle $AÔB$ .

[3]

a.i.

Find the area of the shaded segment.

[5]

a.ii.

Find the area of a circle with radius $4.5 m$ .

[2]

b.i.

Find the area of the field that can be reached by the goat.

[3]

b.ii.

Find the value of $t$ at which the goat is eating grass at the greatest rate.

[2]

Markscheme

$(\frac{1}{2} AÔB =) arccos (\frac{4}{4.5}) = 27.266 \dots$ (M1)(A1)

$AÔB = 54.532 \dots \approx 54.5 °$ ( $0.951764 \dots \approx 0.952$ radians) A1

Note: Other methods may be seen; award (M1)(A1) for use of a correct trigonometric method to find an appropriate angle and then A1 for the correct answer.

[3 marks]

a.i.

finding area of triangle

EITHER

area of triangle $= \frac{1}{2} \times 4 . 5^{2} \times \sin (54.532 \dots)$ (M1)

Note: Award M1 for correct substitution into formula.

$= 8.24621 \dots \approx 8.25 m^{2}$ (A1)

$AB = 2 \times \sqrt{4 . 5^{2} - 4^{2}} = 4.1231 \dots$

area triangle $= \frac{4.1231 \dots \times 4}{2}$ (M1)

$= 8.24621 \dots \approx 8.25 m^{2}$ (A1)

finding area of sector

EITHER

area of sector $= \frac{54.532 \dots}{360} \times π \times 4 . 5^{2}$ (M1)

$= 9.63661 \dots \approx 9.64 m^{2}$ (A1)

area of sector $= \frac{1}{2} \times 0.9517641 \dots \times 4 . 5^{2}$ (M1)

$= 9.63661 \dots \approx 9.64 m^{2}$ (A1)

THEN

area of segment $= 9.63661 \dots - 8.24621 \dots$

$= 1.39 m^{2} (1.39040 \dots)$ A1

[5 marks]

a.ii.

$π \times 4 . 5^{2}$ (M1)

$63.6 m^{2} (63.6172 \dots m^{2})$ A1

[2 marks]

b.i.

METHOD 1

$4 \times 1.39040 . . . (5.56160)$ (A1)

subtraction of four segments from area of circle (M1)

$= 58.1 m^{2} (58.055 \dots)$ A1

METHOD 2

$4 (0.5 \times 4 . 5^{2} \times \sin 54.532 \dots) + 4 (\frac{35.4679}{360} \times π \times 4 . 5^{2})$ (M1)

$= 32.9845 \dots + 25.0707$ (A1)

$= 58.1 m^{2} (58.055 \dots)$ A1

[3 marks]

b.ii.

sketch of $\frac{d V}{d t}$ OR $\frac{d V}{d t} = 0.110363 \dots$ OR attempt to find where $\frac{d^{2} V}{d t^{2}} = 0$ (M1)

$t = 1$ hour A1

[2 marks]

Examiners report

Part (a)(i) proved to be difficult for many candidates. About half of the candidates managed to correctly find the angle $A \hat{O} B$ . A variety of methods were used: cosine to find half of $A \hat{O} B$ then double it; sine to find angle $A \hat{O} B$ , then find half of A $A \hat{O} B$ and double it; Pythagoras to find half of AB and then sine rule to find half of angle $A \hat{O} B$ then double it; Pythagoras to find half of AB, then double it and use cosine rule to find angle $A \hat{O} B$ . Many candidates lost a mark here due to premature rounding of an intermediate value and hence the final answer was not correct (to three significant figures).

In part (a)(ii) very few candidates managed to find the correct area of the shaded segment and include the correct units. Some only found the area of the triangle or the area of the sector and then stopped.

In part (b)(i), nearly all candidates managed to find the area of a circle.

In part (b)(ii), finding the area of the field reached by the goat proved troublesome for most of the candidates. It appeared as if the candidates did not fully understand the problem. Very few candidates realized the connection to part (a)(ii).

Part (c) was accessed by only a handful of candidates. The candidates could simply have graphed the function on their GDC to find the greatest value, but most did not realize this.

a.i.

[N/A]

a.ii.

[N/A]

b.i.

[N/A]

b.ii.

[N/A]