| Date | May 2017 | Marks available | 7 | Reference code | 17M.2.AHL.TZ1.H_10 |
| Level | Additional Higher Level | Paper | Paper 2 | Time zone | Time zone 1 |
| Command term | Determine | Question number | H_10 | Adapted from | N/A |
Question
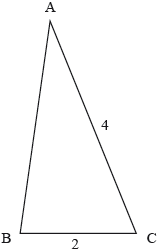
In triangle and .
Consider the possible triangles with .
Consider the case where , the length of QR is not fixed at 8 cm.
Use the cosine rule to show that .
Calculate the two corresponding values of PQ.
Hence, find the area of the smaller triangle.
Determine the range of values of for which it is possible to form two triangles.
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
M1A1
AG
[2 marks]
EITHER
(M1)
OR
using the sine rule (M1)
THEN
or A1
A1
[3 marks]
M1A1
A1
[3 marks]
METHOD 1
EITHER
discriminant M1
A1
M1
A1
OR
construction of a right angle triangle (M1)
M1(A1)
hence for two triangles R1
THEN
A1
to ensure two positive solutions or valid geometric argument R1
A1
METHOD 2
diagram showing two triangles (M1)
M1A1
one right angled triangle when (A1)
for two triangles R1
for two triangles A1
A1
[7 marks]