IB Questionbank

User interface language: English | Español

Date	May 2017	Marks available	3	Reference code	17M.2.AHL.TZ1.H_10
Level	Additional Higher Level	Paper	Paper 2	Time zone	Time zone 1
Command term	Find and Hence	Question number	H_10	Adapted from	N/A

Question

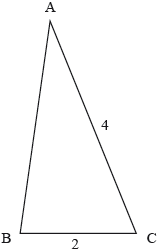
In triangle ${\text{PQR, PR}} = 12{\text{ cm, QR}} = p{\text{ cm, PQ}} = r{\text{ cm}}$ and ${\rm{Q\hat PR}} = 30^\circ$ .

Consider the possible triangles with ${\text{QR}} = 8{\text{ cm}}$ .

Consider the case where $p$ , the length of QR is not fixed at 8 cm.

Use the cosine rule to show that ${r^2} - 12\sqrt 3 r + 144 - {p^2} = 0$ .

[2]

Calculate the two corresponding values of PQ.

[3]

Hence, find the area of the smaller triangle.

[3]

Determine the range of values of $p$ for which it is possible to form two triangles.

[7]

Markscheme

* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.

${p^2} = {12^2} + {r^2} - 2 \times 12 \times r \times \cos (30^\circ )$ M1A1

${r^2} - 12\sqrt 3 r + 144 - {p^2} = 0$ AG

[2 marks]

EITHER

${r^2} - 12\sqrt 3 r + 80 = 0$ (M1)

using the sine rule (M1)

THEN

${\text{PQ}} = 5.10{\text{ }}({\text{cm}})$ or A1

${\text{PQ}} = 15.7{\text{ }}({\text{cm}})$ A1

[3 marks]

${\text{area}} = \frac{1}{2} \times 12 \times 5.1008 \ldots \times \sin (30^\circ )$ M1A1

$= 15.3{\text{ }}({\text{c}}{{\text{m}}^2})$ A1

[3 marks]

METHOD 1

EITHER

${r^2} - 12\sqrt 3 r + 144 - {p^2} = 0$

discriminant $= {\left( {12\sqrt 3 } \right)^2} - 4 \times (144 - {p^2})$ M1

$= 4({p^2} - 36)$ A1

$({p^2} - 36) > 0$ M1

$p > 6$ A1

construction of a right angle triangle (M1)

$12\sin 30^\circ = 6$ M1(A1)

hence for two triangles $p > 6$ R1

THEN

$p < 12$ A1

$144 - {p^2} > 0$ to ensure two positive solutions or valid geometric argument R1

$\therefore 6 < p < 12$ A1

METHOD 2

diagram showing two triangles (M1)

$12\sin 30^\circ = 6$ M1A1

one right angled triangle when $p = 6$ (A1)

$\therefore p > 6$ for two triangles R1

$p < 12$ for two triangles A1

$6 < p < 12$ A1

[7 marks]

Examiners report

[N/A]

Syllabus sections

Topic 3—Geometry and trigonometry » SL 3.2—2d and 3d trig

Show 99 related questions

18M.2.SL.TZ2.T_5a.ii:
Use Giovanni's diagram to calculate the length of AX.
22M.3.AHL.TZ2.2c:
State why the cost for installing the cable between $A$ and $F$ would be higher than between the other buildings.
22M.3.AHL.TZ2.2b:
Find the cost per metre of installing this cable.
22M.1.SL.TZ1.1:
The front view of a doghouse is made up of a square with an isosceles triangle on top.

The doghouse is $1.35 m$ high and $0.9 m$ wide, and sits on a square base.

The top of the rectangular surfaces of the roof of the doghouse are to be painted.

Find the area to be painted.
22M.2.SL.TZ2.3f:
Hence find the area of triangle $XYZ$ .
22M.1.SL.TZ2.3b:
Calculate the distance from Camera $2$ to the centre of the cash register.
18N.2.AHL.TZ0.H_7:
Boat A is situated 10km away from boat B, and each boat has a marine radio transmitter on board. The range of the transmitter on boat A is 7km, and the range of the transmitter on boat B is 5km. The region in which both transmitters can be detected is represented by the shaded region in the following diagram. Find the area of this region.
22M.2.SL.TZ1.4a.ii:
Find the area of the shaded segment.
17N.1.SL.TZ0.T_10b:
Write down the angle of elevation of B from E.
22M.2.AHL.TZ1.2a.ii:
Find the area of the shaded segment.
19N.2.SL.TZ0.T_5a:
Find the length of $AD$ .
21N.1.SL.TZ0.2b:
Find the area of the Bermuda Triangle.
22M.2.SL.TZ1.4a.i:
Find the angle $AÔB$ .
21N.2.SL.TZ0.4b.ii:
Hence or otherwise, show that the volume of the reservoir is $29 600 m^{3}$ .
22M.1.SL.TZ2.3a:
Determine the angle of depression from Camera $1$ to the centre of the cash register. Give your answer in degrees.
22M.1.SL.TZ2.3c:
Without further calculation, determine which camera has the largest angle of depression to the centre of the cash register. Justify your response.
22M.3.AHL.TZ2.2a:
Find $AF$ .
22M.1.SL.TZ1.2a:
Find the length of the rope connecting $A$ to $F$ .
22M.1.SL.TZ1.2b:
Find $FÂO$ , the angle the rope makes with the ground.
22M.2.AHL.TZ1.2a.i:
Find the angle $AÔB$ .
19M.2.SL.TZ2.T_2b.ii:
Find the size of angle ${\text{C}}\mathop {\text{A}}\limits^ \wedge {\text{D}}$ .
17N.2.SL.TZ0.T_3c:
Find the area of ABCD.
18M.2.SL.TZ1.T_1b:
Calculate the total volume of the barn.
17N.1.SL.TZ0.T_10c:
Find the vertical height of B above the ground.
19M.1.SL.TZ1.T_8a:
Draw and label the angle of depression on the diagram.
17M.2.SL.TZ1.T_2a.i:
Write down an equation for the area of ABCDE using the above information.
18M.2.SL.TZ1.T_1d:
Calculate the length of AE.
18M.2.SL.TZ2.S_2b:
Find DC.
18M.2.SL.TZ1.T_1e:
Show that Farmer Brown is incorrect.
19N.2.SL.TZ0.T_2b:
Find the coordinates of point $C$ .
19N.2.SL.TZ0.T_5d:
Determine whether the rope can extend into the triangular plot of land, $ACD$ . Justify your answer.
19N.2.SL.TZ0.T_2a:
Find the gradient of $L_{1}$ .
18M.2.SL.TZ2.T_5b:
Find the percentage error on Giovanni’s diagram.
19N.2.SL.TZ0.T_2d:
Find the value of $k$ .
SPM.1.SL.TZ0.14b:
Point B on the ground is 5 m from point E at the entrance to Ollie’s house. He is 1.8 m tall and is standing at point D, below the sensor. He walks towards point B.

Find the distance Ollie is from the entrance to his house when he first activates the sensor.
17M.2.SL.TZ1.T_2d:
Find the length of the perimeter of ABCDE.
16N.2.SL.TZ0.T_5c:
the area of triangle ABD;
19M.1.AHL.TZ1.H_4b:
Find the two possible values for the length of the third side.
18N.2.SL.TZ0.S_7a:
Let SR = $x$ . Use the cosine rule to show that ${x^2} - \left( {76\,{\text{cos}}\,43^\circ } \right)x + 420 = 0$ .
17N.2.SL.TZ0.T_3d.ii:
Find the percentage error in Abdallah’s estimate.
18M.2.SL.TZ1.T_1a:
Calculate the area of triangle EAD.
21M.2.SL.TZ2.2c:
Find the area of triangle $DCE$ .
19M.1.AHL.TZ1.H_4a:
Show that ${\text{sin}}\,\theta = \frac{{\sqrt {15} }}{4}$ .
17N.1.SL.TZ0.T_10a:
Find the length of EB.
19N.2.SL.TZ0.T_2e:
Find the distance between points $M$ and $N$ .
18M.2.SL.TZ1.T_1f:
Calculate the total length of metal required for one support.
20N.1.SL.TZ0.S_2a:
Given that $A \hat{B} C$ is acute, find $\sin θ$ .
20N.2.SL.TZ0.T_3b:
Show that angle $EDC = 48.0 °$ , correct to three significant figures.
18M.2.SL.TZ2.T_5a.iii:
Use Giovanni's diagram to find the length of BX, the horizontal displacement of the Tower.
16N.2.SL.TZ0.T_5b:
the size of angle DAB;
20N.1.SL.TZ0.S_2b:
Find $\cos (2 \times C \hat{A} B)$ .
19N.2.SL.TZ0.T_2c:
Find the equation of $L_{2}$ . Give your answer in the form $a x + b y + d = 0$ , where $a, b, d \in ℤ$ .
17M.2.AHL.TZ2.H_4a:
Find the set of values of $k$ that satisfy the inequality ${k^2} - k - 12 < 0$ .
18M.2.SL.TZ2.T_5c:
Giovanni adds a point D to his diagram, such that BD = 45 m, and another triangle is formed.

Find the angle of elevation of A from D.
18M.2.SL.TZ2.T_5a.i:
Use Giovanni’s diagram to show that angle ABC, the angle at which the Tower is leaning relative to the
horizontal, is 85° to the nearest degree.
21M.2.SL.TZ1.2a:
Find the size of angle $A \hat{O} B$ in degrees.
19N.2.SL.TZ0.T_5c:
Calculate the area of the triangular plot of land $ABC$ .
17M.2.AHL.TZ1.H_10a:
Use the cosine rule to show that ${r^2} - 12\sqrt 3 r + 144 - {p^2} = 0$ .
19N.2.SL.TZ0.T_5b:
Find the size of $A \hat{B} C$ .
17M.2.SL.TZ1.T_2a.ii:
Show that the equation in part (a)(i) simplifies to $3{x^2} + 19x - 414 = 0$ .
16N.2.SL.TZ0.T_5d:
the area of quadrilateral ABCD;
17M.2.SL.TZ1.T_2b:
Find the length of CD.
17M.2.AHL.TZ2.H_4b:
The triangle ABC is shown in the following diagram. Given that $\cos B < \frac{1}{4}$ , find the range of possible values for AB.
17M.2.SL.TZ1.T_2e:
Calculate the length of CF.
16N.2.SL.TZ0.T_5f:
the length of the fence, BP.
18M.2.SL.TZ2.S_2a:
Find DB.
20N.2.SL.TZ0.T_3d:
Pedro draws a circle, with centre at point $E$ , passing through point $C$ . Part of the circle is shown in the diagram.

Show that point $A$ lies outside this circle. Justify your reasoning.
SPM.1.SL.TZ0.14a:
Find CÂB.
17N.2.SL.TZ0.T_3b:
Calculate angle ${\rm{B\hat CD}}$ .
19M.2.SL.TZ2.T_2c:
Find the size of angle ${\text{A}}\mathop {\text{C}}\limits^ \wedge {\text{D}}$ .
16N.2.SL.TZ0.T_5a:
the length of BD;
21M.2.SL.TZ1.2b:
Find the distance between points $A$ and $B$ .
20N.2.SL.TZ0.T_3c:
Calculate the area of triangle $BDC$ .
18M.2.SL.TZ1.T_1c:
Calculate the length of MN.
17N.2.SL.TZ0.T_3d.i:
Calculate Abdallah’s estimate for the area.
16N.2.SL.TZ0.T_5e:
the length of AP;
17M.2.SL.TZ1.S_5:
The following diagram shows the chord [AB] in a circle of radius 8 cm, where ${\text{AB}} = 12{\text{ cm}}$ .

Find the area of the shaded segment.
21M.2.SL.TZ2.2b:
Find $DE$ .
21M.2.SL.TZ2.2d:
Estimate $DF$ . You may assume the highway has a width of zero.
17N.2.SL.TZ0.T_3a:
Show that ${\text{BD}} = 93{\text{ m}}$ correct to the nearest metre.
19M.2.AHL.TZ2.H_1:
In triangle ABC, AB = 5, BC = 14 and AC = 11.

Find all the interior angles of the triangle. Give your answers in degrees to one decimal place.
17M.2.AHL.TZ1.H_10b:
Calculate the two corresponding values of PQ.
17M.2.SL.TZ1.T_2c:
Show that angle ${\rm{B\hat AE}} = 67.4^\circ$ , correct to one decimal place.
19N.2.SL.TZ0.T_2f:
Given that the length of $AM$ is $\sqrt{45}$ , find the area of triangle $ANC$ .
17M.2.AHL.TZ1.H_10d:
Determine the range of values of $p$ for which it is possible to form two triangles.
20N.2.SL.TZ0.T_3a:
Calculate the length of $BD$ .
EXN.1.SL.TZ0.11a:
Find the area of the field.
EXN.1.SL.TZ0.11b:
The farmer would like to divide the field into two equal parts by constructing a straight fence from $A$ to a point $D$ on $[BC]$ .

Find $BD$ . Fully justify any assumptions you make.
21M.1.SL.TZ2.9a:
A footpath is to be laid around the curved side of the lawn. Find the length of the footpath.
21M.1.SL.TZ1.9:
A triangular field $ABC$ is such that $AB = 56 m$ and $BC = 82 m$ , each measured correct to the nearest metre, and the angle at $B$ is equal to $105 °$ , measured correct to the nearest $5 °$ .

Calculate the maximum possible area of the field.
21M.1.SL.TZ2.9b:
Find the area of the lawn.
21M.2.SL.TZ2.2a:
Find the size of $AĈB$ .
21M.2.SL.TZ2.5a:
Given that $\sin 60 ° = \frac{\sqrt{3}}{2}$ , show that the area of the base of the box is equal to $\frac{3 \sqrt{3} x^{2}}{2}$ .
21N.1.AHL.TZ0.11:
The following diagram shows a corner of a field bounded by two walls defined by lines $L_{1}$ and $L_{2}$ . The walls meet at a point $A$ , making an angle of $40 °$ .

Farmer Nate has $7 m$ of fencing to make a triangular enclosure for his sheep. One end of the fence is positioned at a point $B$ on $L_{2}$ , $10 m$ from $A$ . The other end of the fence will be positioned at some point $C$ on $L_{1}$ , as shown on the diagram.

He wants the enclosure to take up as little of the current field as possible.

Find the minimum possible area of the triangular enclosure $ABC$ .
21N.2.SL.TZ0.4a:
Find the angle of depression from $M$ to $N$ .
21N.2.SL.TZ0.4b.i:
Find $CV$ .
21N.2.SL.TZ0.4c:
By finding an appropriate value, determine whether Joshua is correct.
21N.2.SL.TZ0.4d:
To avoid water leaking into the ground, the five interior sides of the reservoir have been painted with a watertight material.

Find the area that was painted.
21N.1.SL.TZ0.2a:
Calculate the value of $θ$ , the measure of angle $MŜB$ .

Hide related questions

Topic 3—Geometry and trigonometry » AHL 3.8—Unit circle, Pythag identity, solving trig equations graphically

Topic 3—Geometry and trigonometry

Question

Markscheme

Examiners report

Syllabus sections

View options