| Date | May 2017 | Marks available | 7 | Reference code | 17M.3.AHL.TZ0.Hdm_2 |
| Level | Additional Higher Level | Paper | Paper 3 | Time zone | Time zone 0 |
| Command term | Find | Question number | Hdm_2 | Adapted from | N/A |
Question
The weights of the edges in the complete graph are given in the following table.
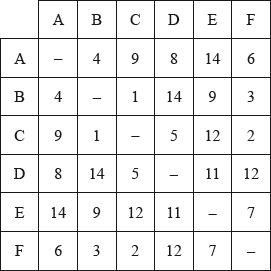
Starting at A , use the nearest neighbour algorithm to find an upper bound for the travelling salesman problem for .
By first deleting vertex A , use the deleted vertex algorithm together with Kruskal’s algorithm to find a lower bound for the travelling salesman problem for .
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
the edges are traversed in the following order
AB A1
BC
CF A1
FE
ED A1
DA A1
A1
[5 marks]
having deleted A, the order in which the edges are added is
BC A1
CF A1
CD A1
EF A1
Note: Accept indication of the correct order on a diagram.
to find the lower bound, we now reconnect A using the two edges with the lowest weights, that is AB and AF (M1)(A1)
A1
Note: Award (M1)(A1)A1 for obtained either from an incorrect order of correct edges or where order is not indicated.
[7 marks]
Examiners report
Syllabus sections
-
22M.3.AHL.TZ1.2f.iii:
A sewer inspector needs to plan the shortest possible route through each of the connections between different locations. Determine an appropriate start point and an appropriate end point of the inspection route.
Note that the fact that each location is connected to itself does not correspond to a sewer that needs to be inspected.
-
22M.3.AHL.TZ2.2f:
Starting at , use the nearest neighbour algorithm to find the upper bound for the installation cost of a computer network in the form of a Hamiltonian cycle.
Note: Although the graph is not complete, in this instance it is not necessary to form a table of least distances.
-
EXM.1.AHL.TZ0.23b:
Find the lowest cost road system and state the cost of building it. Show clearly the steps of the algorithm.
-
EXM.1.AHL.TZ0.39b:
What is the total weight of the tree?
-
EXM.1.AHL.TZ0.40:
The weights of the edges of a complete graph G are shown in the following table.
Starting at B, use Prim’s algorithm to find and draw a minimum spanning tree for G. Your solution should indicate the order in which the vertices are added. State the total weight of your tree.
-
18M.3.AHL.TZ0.Hdm_1b:
Write down an Eulerian trail in G.
-
18M.3.AHL.TZ0.Hdm_1c.iii:
Calculate the total weight of the solution.
-
SPM.2.AHL.TZ0.5f:
Use the nearest neighbour algorithm to find an upper bound for the cost of the trip.
-
EXM.2.AHL.TZ0.2c.ii:
Sketch the tracks that are to be tarmacked.
-
EXM.1.AHL.TZ0.23a:
Name an algorithm that will allow Sameer to find the lowest cost road system.
-
22M.3.AHL.TZ2.2g:
By deleting , use the deleted vertex algorithm to find the lower bound for the installation cost of the cycle.
-
EXM.1.AHL.TZ0.24b:
Starting at A, use Prim’s algorithm to find and draw the minimum spanning tree for G.
Your solution should indicate clearly the way in which the tree is constructed.
-
22M.3.AHL.TZ2.2d.ii:
Hence find the minimum installation cost for the cables that would allow all the buildings to be part of the computer network.
-
22M.3.AHL.TZ2.2e:
State why a path that forms a Hamiltonian cycle does not always form an Eulerian circuit.
-
22M.3.AHL.TZ2.2d.i:
By using Kruskal’s algorithm, find the minimum spanning tree for , showing clearly the order in which edges are added.
-
EXM.2.AHL.TZ0.17a:
Draw a graph to represent this map.
-
EXM.2.AHL.TZ0.17d.i:
an Eulerian circuit.
-
EXM.2.AHL.TZ0.17d.ii:
an Eulerian trail.
-
EXM.2.AHL.TZ0.18b.i:
Define an Eulerian circuit.
-
EXM.2.AHL.TZ0.18c.ii:
Explain why it is not possible to have a Hamiltonian cycle in G.
-
EXM.2.AHL.TZ0.19d:
Show that the lower bound you have obtained is not the best possible for the solution to the travelling salesman problem for G.
-
EXM.1.AHL.TZ0.39a:
Use Prim’s algorithm to draw a minimum spanning tree starting at M.
-
EXM.2.AHL.TZ0.19a:
Find the total number of Hamiltonian cycles in G, starting at vertex A. Explain your answer.
-
18N.3.AHL.TZ0.Hdm_4a:
State, with a reason, whether or not G has an Eulerian circuit.
-
EXM.1.AHL.TZ0.24a.ii:
Find the number of distinct walks of length 4 beginning and ending at A.
-
18N.3.AHL.TZ0.Hdm_4c:
Use a suitable algorithm to show that the minimum time in which Mr José can get from A to E is 13 minutes.
-
SPM.2.AHL.TZ0.5c:
Using your answer to part (b), find the number of different ways to travel from and return to city A in exactly 6 flights.
-
EXM.2.AHL.TZ0.17e:
Find the number of walks of length 4 from E to F.
-
18M.3.AHL.TZ0.Hdm_1a.ii:
State what feature of G ensures that G does not have an Eulerian circuit.
-
18M.3.AHL.TZ0.Hdm_1a.i:
State what feature of G ensures that G has an Eulerian trail.
-
17M.3.AHL.TZ0.Hdm_3a.i:
In the context of graph theory, explain briefly what is meant by a circuit;
-
EXM.2.AHL.TZ0.17c:
List the degrees of each of the vertices.
-
17N.3.AHL.TZ0.Hdm_1c:
By first removing library C, use the deleted vertex algorithm, to find a lower bound for Mathilde’s minimum travelling distance.
-
EXM.1.AHL.TZ0.1a:
Find with a reason, the value of .
-
EXM.2.AHL.TZ0.2b.iii:
Using Prim’s algorithm starting at vertex F.
-
EXM.2.AHL.TZ0.2c.i:
State the total minimum length of the tracks that have to be tarmacked.
-
SPM.2.AHL.TZ0.5d:
State whether or not it is possible to travel from and return to city A in exactly 6 flights, having visited each of the other 5 cities exactly once. Justify your answer.
-
SPM.2.AHL.TZ0.5e:
Find the values of and .
-
EXM.1.AHL.TZ0.38:
The diagram below shows a weighted graph.
Use Prim’s algorithms to find a minimal spanning tree, starting at J. Draw the tree, and find its total weight.
-
EXM.1.AHL.TZ0.41:
The weights of the edges in a simple graph G are given in the following table.
Use Prim’s Algorithm, starting with vertex F, to find and draw the minimum spanning tree for G. Your solution should indicate the order in which the edges are introduced.
-
EXM.2.AHL.TZ0.18a:
Draw the graph of G.
-
EXM.2.AHL.TZ0.18c.i:
Define a Hamiltonian cycle.
-
EXM.1.AHL.TZ0.37:
In this part, marks will only be awarded if you show the correct application of the required algorithms, and show all your working.
In an offshore drilling site for a large oil company, the distances between the planned wells are given below in metres.
It is intended to construct a network of paths to connect the different wells in a way that minimises the sum of the distances between them.
Use Prim’s algorithm, starting at vertex 3, to find a network of paths of minimum total length that can span the whole site.
-
EXM.2.AHL.TZ0.18b.ii:
Write down an Eulerian circuit in G starting at P.
-
19N.3.AHL.TZ0.Hdm_1a:
By deleting , use the deleted vertex algorithm to find a lower bound for the length of a route that visits every shop, starting and finishing at .
-
SPM.2.AHL.TZ0.5g:
By deleting vertex A, use the deleted vertex algorithm to find a lower bound for the cost of the trip.
-
17M.3.AHL.TZ0.Hdm_3b:
The graph has six vertices and an Eulerian circuit. Determine whether or not its complement can have an Eulerian circuit.
-
20N.1.AHL.TZ0.F_2a:
Verify that satisfies the handshaking lemma.
-
EXM.1.AHL.TZ0.36:
Apply Prim’s algorithm to the weighted graph given below to obtain the minimal spanning tree starting with the vertex A.
Find the weight of the minimal spanning tree.
-
EXM.2.AHL.TZ0.2b.ii:
Using Prim’s algorithm starting at vertex A.
-
EXM.1.AHL.TZ0.24a.i:
Write down the adjacency matrix for G.
-
17N.3.AHL.TZ0.Hdm_1a:
Draw the weighted graph .
-
SPM.2.AHL.TZ0.5a:
Show the direct flights between the cities as a graph.
-
EXM.1.AHL.TZ0.1b:
If the total length of the minimal spanning tree is 14, find the value of .
-
EXM.2.AHL.TZ0.2b.i:
Using Kruskal’s algorithm.
-
EXM.2.AHL.TZ0.2a:
Briefly explain the two differences in the application of Prim’s and Kruskal’s algorithms for finding a minimum spanning tree in a weighted connected graph.
-
17M.3.AHL.TZ0.Hdm_3a.ii:
In the context of graph theory, explain briefly what is meant by an Eulerian circuit.
-
18N.3.AHL.TZ0.Hdm_4b:
Use Kruskal’s algorithm to find a minimum spanning tree for G, stating its total weight. Indicate clearly the order in which the edges are added.
-
16N.3.AHL.TZ0.Hdm_4a:
(i) Draw the graph including the weights of all the edges.
(ii) Use the nearest-neighbour algorithm, starting at vertex , to find a Hamiltonian cycle.
(iii) Hence, find an upper bound to the travelling salesman problem for this weighted graph.
-
16N.3.AHL.TZ0.Hdm_4d:
By splitting the weight of the edge into two parts or otherwise, show that all Hamiltonian cycles of have the same total weight, equal to the answer found in (c)(ii).
-
EXM.2.AHL.TZ0.18d.ii:
Which pairs of distinct vertices have more than 15 walks of length 3 between them?
-
EXM.2.AHL.TZ0.19b.ii:
Hence, find a lower bound for the travelling salesman problem for G.
-
EXM.2.AHL.TZ0.19c:
Give an upper bound for the travelling salesman problem for the graph above.
-
EXM.2.AHL.TZ0.19b.i:
Find a minimum spanning tree for the subgraph obtained by deleting A from G.
-
19N.3.AHL.TZ0.Hdm_1b:
Starting from , use the nearest-neighbour algorithm to find a route which gives an upper bound for this problem and calculate its length.
-
18M.3.AHL.TZ0.Hdm_1c.ii:
Starting and finishing at B, find a solution to the Chinese postman problem for G.
-
20N.1.AHL.TZ0.F_2c:
State, giving a reason, whether contains an Eulerian circuit.
-
20N.3.AHL.TZ0.Hdm_2a.i:
Use Dijkstra’s algorithm to find the shortest time to travel from to , clearly showing how the algorithm has been applied.
-
20N.3.AHL.TZ0.Hdm_2a.ii:
Hence write down the shortest path from to .
-
20N.1.AHL.TZ0.F_2b:
Show that cannot be redrawn as a planar graph.
-
16N.3.AHL.TZ0.Hdm_4c:
(i) Use the nearest-neighbour algorithm, starting at vertex , to find a Hamiltonian cycle.
(ii) Hence find and simplify an expression in , for an upper bound to the travelling salesman problem for this weighted graph.
-
EXM.2.AHL.TZ0.17b:
Write down the adjacency matrix of the graph.
-
SPM.2.AHL.TZ0.5b:
Write down the adjacency matrix for this graph.
-
17M.3.AHL.TZ0.Hdm_2a:
Starting at A , use the nearest neighbour algorithm to find an upper bound for the travelling salesman problem for .
-
20N.3.AHL.TZ0.Hdm_2b:
A new road is constructed that allows Christine to travel from to in minutes. If Christine starts from home and uses this new road her minimum travel time to is reduced, but her minimum travel time to remains the same.
Find the possible values of .
-
EXM.1.AHL.TZ0.1c:
Hence, state, with a reason, what can be deduced about the values of , , .
-
17N.3.AHL.TZ0.Hdm_1b:
Starting at library D use the nearest-neighbour algorithm, to find an upper bound for Mathilde’s minimum travelling distance. Indicate clearly the order in which the edges are selected.
-
17M.3.AHL.TZ0.Hdm_3c:
Find an example of a graph , with five vertices, such that and its complement both have an Eulerian trail but neither has an Eulerian circuit. Draw and as your solution.
-
18N.3.AHL.TZ0.Hdm_4d:
Find the minimum time it takes Mr José to patrol the resort if he has to walk along every road at least once, starting and ending at A. State clearly which roads need to be repeated.
-
21M.1.AHL.TZ1.10b:
Describe how an improved lower bound might be found.
-
21M.1.AHL.TZ1.10a.ii:
Hence find a lower bound for the travelling time needed to visit all the oil rigs.
-
16N.3.AHL.TZ0.Hdm_4b:
Consider the graph . Use the deleted vertex algorithm, with as the deleted vertex, to find a lower bound to the travelling salesman problem for this weighted graph.
-
EXM.2.AHL.TZ0.18d.i:
Find the number of walks of length 5 from P to Q.
-
21M.1.AHL.TZ2.11a:
Musab starts and finishes from the village bus-stop at . Determine the total distance Musab will need to walk.
-
21M.1.AHL.TZ1.10a.i:
Use Prim’s algorithm to find the weight of the minimum spanning tree of the subgraph of obtained by deleting and starting at . List the order in which the edges are selected.
-
21M.1.AHL.TZ2.11b:
Instead of having to catch the bus to the village, Musab’s sister offers to drop him off at any junction and pick him up at any other junction of his choice.
Explain which junctions Musab should choose as his starting and finishing points.
-
EXN.1.AHL.TZ0.11:
Nymphenburg Palace in Munich has extensive grounds with points of interest (stations) within them.
These nine points, along with the palace, are shown as the vertices in the graph below. The weights on the edges are the walking times in minutes between each of the stations and the total of all the weights is minutes.
Anders decides he would like to walk along all the paths shown beginning and ending at the Palace (vertex A).
Use the Chinese Postman algorithm, clearly showing all the stages, to find the shortest time to walk along all the paths.

