| Date | November 2016 | Marks available | 3 | Reference code | 16N.3.AHL.TZ0.Hdm_4 |
| Level | Additional Higher Level | Paper | Paper 3 | Time zone | Time zone 0 |
| Command term | Show that | Question number | Hdm_4 | Adapted from | N/A |
Question
The simple, complete graph has vertices . The weight of the edge from to is given by the number .
Consider the general graph .
(i) Draw the graph including the weights of all the edges.
(ii) Use the nearest-neighbour algorithm, starting at vertex , to find a Hamiltonian cycle.
(iii) Hence, find an upper bound to the travelling salesman problem for this weighted graph.
Consider the graph . Use the deleted vertex algorithm, with as the deleted vertex, to find a lower bound to the travelling salesman problem for this weighted graph.
(i) Use the nearest-neighbour algorithm, starting at vertex , to find a Hamiltonian cycle.
(ii) Hence find and simplify an expression in , for an upper bound to the travelling salesman problem for this weighted graph.
By splitting the weight of the edge into two parts or otherwise, show that all Hamiltonian cycles of have the same total weight, equal to the answer found in (c)(ii).
Markscheme
* This question is from an exam for a previous syllabus, and may contain minor differences in marking or structure.
(i) 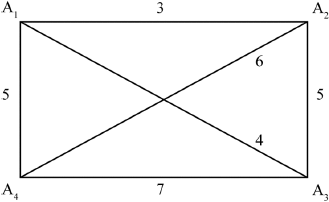 A1A1
A1A1
Note: A1 for the graph, A1 for the weights.
(ii) cycle is A1
(iii) upper bound is A1
[4 marks]
with deleted, (applying Kruskal’s Algorithm) the minimum spanning tree will consist of the edges , of weights 3, 4, 5 (M1)A1
the two edges of smallest weight from are and of weights 6 and 7 (M1)A1
so lower bound is A1
[5 marks]
(i) starting at we go
we now have to take
thus the cycle is A1A1
Note: Final A1 is for .
(ii) smallest edge from is of weight 3, smallest edge from (to a new vertex) is of weight 5, smallest edge from (to a new vertex) is of weight (M1)
weight of is
weight is A1
M1A1
(which is an upper bound) A1
Note: Follow through is not applicable.
[7 marks]
put a marker on each edge so that of the weight belongs to vertex and of the weight belongs to vertex M1
the Hamiltonian cycle visits each vertex once and only once and for vertex there will be weight (belonging to vertex ) both going in and coming out R1
so the total weight will be A1AG
Note: Accept other methods for example induction.
[3 marks]

