| Date | November 2015 | Marks available | 2 | Reference code | 15N.3dm.hl.TZ0.4 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Explain and Write down | Question number | 4 | Adapted from | N/A |
Question
The following diagram shows the graph \(G\).
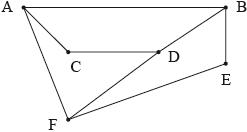
Show that \(G\) is bipartite.
State which two vertices should be joined to make \(G\) equivalent to \({K_{3,{\text{ }}3}}\).
In a planar graph the degree of a face is defined as the number of edges adjacent to that face.
(i) Write down the degree of each of the four faces of \(G\).
(ii) Explain why the sum of the degrees of all the faces is twice the number of edges.
\(H\) is a simple connected planar bipartite graph with \(e\) edges, \(f\) faces, \(v\) vertices and \(v \ge 3\).
Explain why there can be no face in \(H\) of degree
(i) one;
(ii) two;
(iii) three.
Hence prove that for \(H\)
(i) \(e \ge 2f\);
(ii) \(e \le 2v - 4\).
Hence prove that \({K_{3,{\text{ }}3}}\) is not planar.
Markscheme
shading alternate vertices or attempting to list pairs M1
EITHER
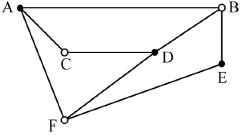 A1
A1
OR
\(ADE\) and \(BCF\) A1
as no two equal shadings are adjacent, the graph is bipartite AG
[2 marks]
\(C\) and \(E\) A1
[1 mark]
(i) degree of each of the four faces is \(4\) A1
(ii) each edge bounds two faces R1
[2 marks]
(i) simple so no loops R1
(ii) simple so no multiple edges (and \(v > 2\)) R1
(iii) bipartite graph so no triangles R1
[3 marks]
(i) \(2e = \sum {\deg (f) \ge 4f} \) R1
\(e \ge 2f\) AG
(ii) if \(H\) is a simple connected planar graph then \(e + 2 = v + f\) M1
\(e + 2 - v \le \frac{1}{2}e\) M1
\(2e + 4 - 2v \le e\)
\(e \le 2v - 4\) AG
[3 marks]
for \({K_{3,{\text{ }}3}}{\text{ }}v = 6\), and \(e = 9\) A1
\(9 \le 2 \times 6 - 4\) is not true, therefore \({K_{3,{\text{ }}3}}\) cannot be planar R1AG
[2 marks]
Total [13 marks]

