| Date | November 2017 | Marks available | 4 | Reference code | 17N.3dm.hl.TZ0.3 |
| Level | HL only | Paper | Paper 3 Discrete mathematics | Time zone | TZ0 |
| Command term | Prove that | Question number | 3 | Adapted from | N/A |
Question
Consider \({\kappa _n}\), a complete graph with \(n\) vertices, \(n \geqslant 2\). Let \(T\) be a fixed spanning tree of \({\kappa _n}\).
Draw the complete bipartite graph \({\kappa _{3,3}}\).
Prove that \({\kappa _{3,3}}\) is not planar.
A connected graph \(G\) has \(v\) vertices. Prove, using Euler’s relation, that a spanning tree for \(G\) has \(v - 1\) edges.
If an edge \(E\) is chosen at random from the edges of \({\kappa _n}\), show that the probability that \(E\) belongs to \(T\) is equal to \(\frac{2}{n}\).
Markscheme
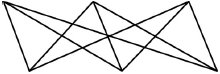 A1
A1
[1 mark]
assume \({\kappa _{3,3}}\) is planar
\({\kappa _{3,3}}\) has no cycles of length 3 R1
use of \(e \leqslant 2v - 4\) M1
\(e = 9\) and \(v = 6\) A1
hence inequality not satisfied 9 \(\not \leqslant \) 8 R1
so \({\kappa _{3,3}}\) is not planar AG
Note: use of \(e \leqslant 3v - 6\) with \(e = 9\) and \(v = 6\) and concluding that this inequality does not show whether \({\kappa _{3,3}}\) is planar or not just gains R1.
[4 marks]
a spanning tree (is planar and) has one face A1
Euler’s relation is \(v - e + f = 2\)
\(v - e + 1 = 2\) M1
\( \Rightarrow e = v - 1\) AG
[2 marks]
\({\kappa _n}\) has \(\left( {\begin{array}{*{20}{c}} n \\ 2 \end{array}} \right)\) edges \(\left( {\frac{{n(n - 1)}}{2}{\text{ edges}}} \right)\) (A1)
\({\text{P}}(E{\text{ belongs to }}T) = \frac{{n - 1}}{{\left( {\frac{{n(n - 1)}}{2}} \right)}}\) M1A1
clear evidence of simplification of the above expression M1
\( = \frac{2}{n}\) AG
[4 marks]

